📕题干
困难
有一根长度为 n 个单位的木棍,棍上从 0 到 n 标记了若干位置。例如,长度为 6 的棍子可以标记如下:
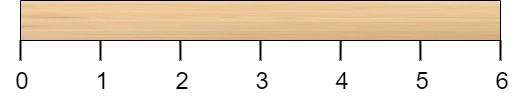
给你一个整数数组 cuts ,其中 cuts[i] 表示你需要将棍子切开的位置。
你可以按顺序完成切割,也可以根据需要更改切割的顺序。
每次切割的成本都是当前要切割的棍子的长度,切棍子的总成本是历次切割成本的总和。对棍子进行切割将会把一根木棍分成两根较小的木棍(这两根木棍的长度和就是切割前木棍的长度)。请参阅第一个示例以获得更直观的解释。
返回切棍子的 最小总成本 。
示例 1:
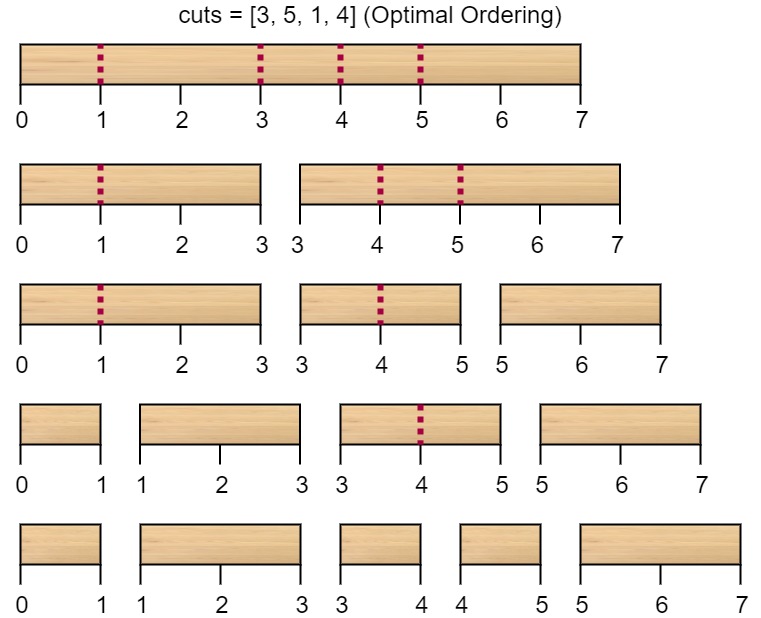
输入:n = 7, cuts = [1,3,4,5] 输出:16 解释:按 [1, 3, 4, 5] 的顺序切割的情况如下所示:第一次切割长度为 7 的棍子,成本为 7 。第二次切割长度为 6 的棍子(即第一次切割得到的第二根棍子),第三次切割为长度 4 的棍子,最后切割长度为 3 的棍子。总成本为 7 + 6 + 4 + 3 = 20 。 而将切割顺序重新排列为 [3, 5, 1, 4] 后,总成本 = 16(如示例图中 7 + 4 + 3 + 2 = 16)。
示例 2:
输入:n = 9, cuts = [5,6,1,4,2] 输出:22 解释:如果按给定的顺序切割,则总成本为 25 。总成本 <= 25 的切割顺序很多,例如,[4, 6, 5, 2, 1] 的总成本 = 22,是所有可能方案中成本最小的。
提示:
2 <= n <= 10^61 <= cuts.length <= min(n - 1, 100)1 <= cuts[i] <= n - 1cuts数组中的所有整数都 互不相同
📖题解
· 法一 动态规划
💻代码
cuts += [0,n]
cuts.sort()
dp = [[float("inf")]* len(cuts) for _ in range(len(cuts))]
for i in range(len(cuts))[::-1]:
for j in range(i+1,len(cuts)):
if j == i+1:
dp[i][j] = 0
else:
dp[i][j] = min(dp[i][k]+dp[k][j] for k in range(i+1,j))+cuts[j]-cuts[i]
return dp[0][-1]🤔思路
用dp[i][j]来表示区间cuts[i],cuts[j]之间的最小成本。然后总结出转移方程$dp[i][j] = \min (dp[i][k]+dp[i][j],k\in (i,j))+cuts[j]-cuts[i]$然后就能写出来了
· 法一 记忆化搜索
💻代码
cuts += [0,n]
cuts.sort()
@cache
def dfs(i,j):
ans = float("inf")
if i + 1 == j:
return 0
for k in range(i+1,j):
ans = min(dfs(i,k)+dfs(k,j),ans)
return ans + cuts[j] - cuts[i]
return dfs(0,len(cuts)-1)🤔思路
用深搜来递归最小花费,原理和动规差不多,然后用@cache来实现记忆化搜索
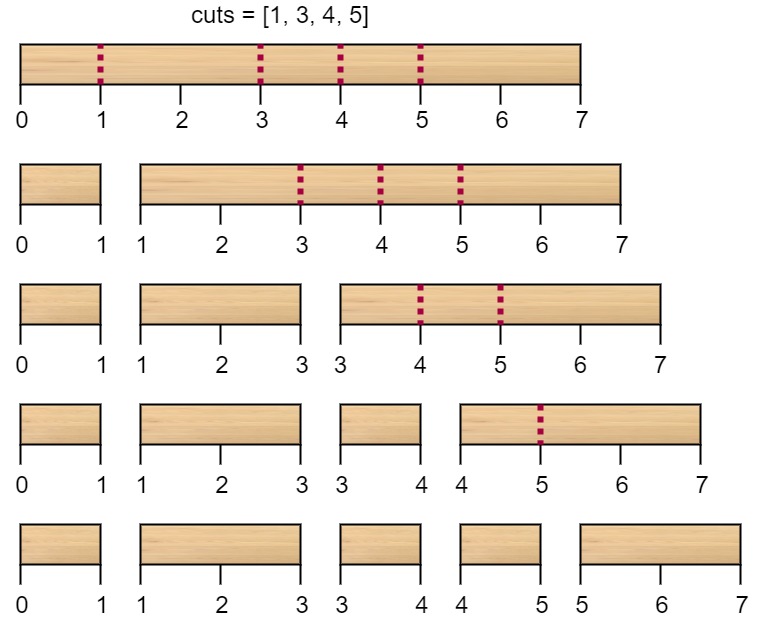 第一次切割长度为 7 的棍子,成本为 7 。第二次切割长度为 6 的棍子(即第一次切割得到的第二根棍子),第三次切割为长度 4 的棍子,最后切割长度为 3 的棍子。总成本为 7 + 6 + 4 + 3 = 20 。
而将切割顺序重新排列为 [3, 5, 1, 4] 后,总成本 = 16(如示例图中 7 + 4 + 3 + 2 = 16)。
第一次切割长度为 7 的棍子,成本为 7 。第二次切割长度为 6 的棍子(即第一次切割得到的第二根棍子),第三次切割为长度 4 的棍子,最后切割长度为 3 的棍子。总成本为 7 + 6 + 4 + 3 = 20 。
而将切割顺序重新排列为 [3, 5, 1, 4] 后,总成本 = 16(如示例图中 7 + 4 + 3 + 2 = 16)。
