RK.39
RP.1483
Reverse
WARMUP | Solved – Spreng
我来签到了
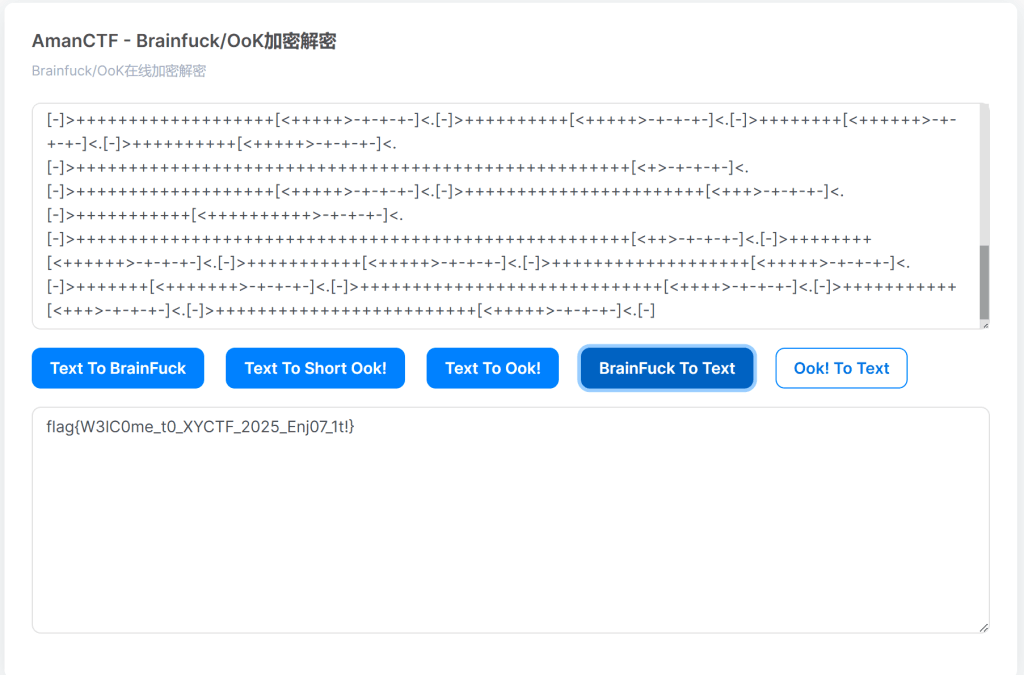
看看VBS里面,源码用char掩盖了。
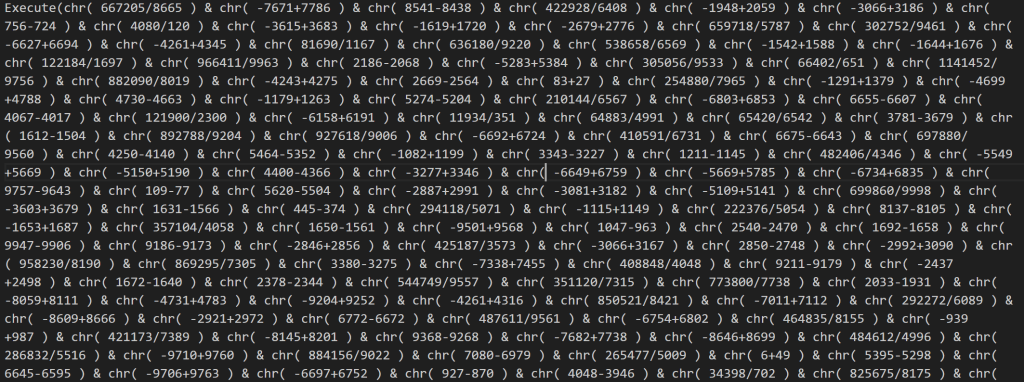
把Execute换成wscript.echo再运行VBS,源码就出来了。
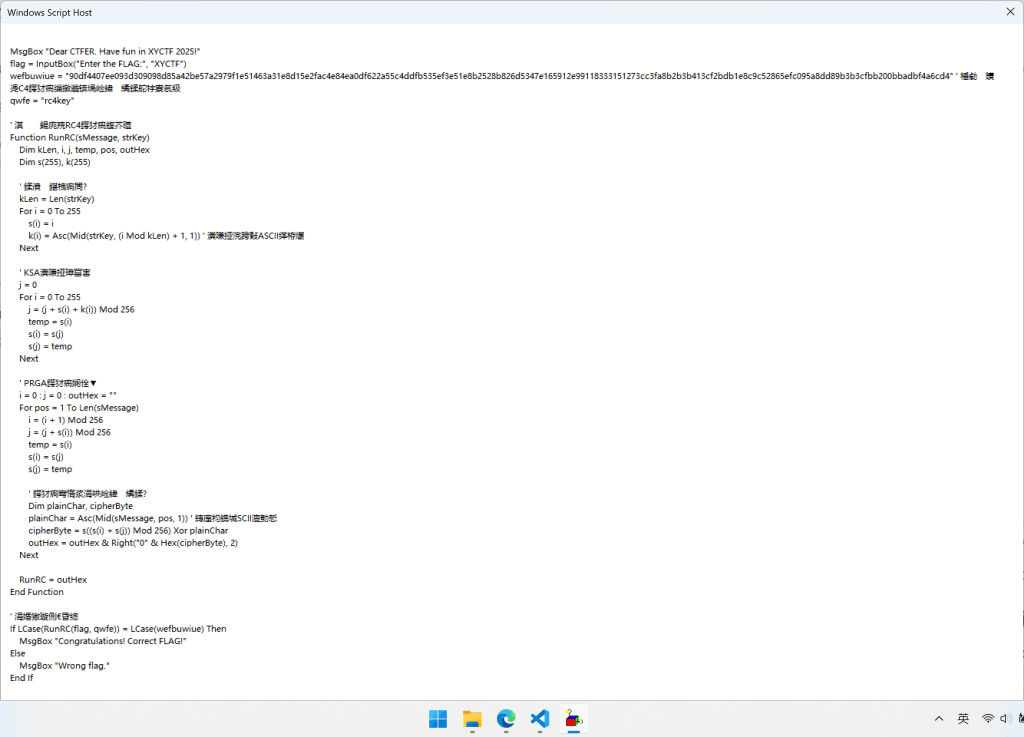
RC4,CyberChef解掉。
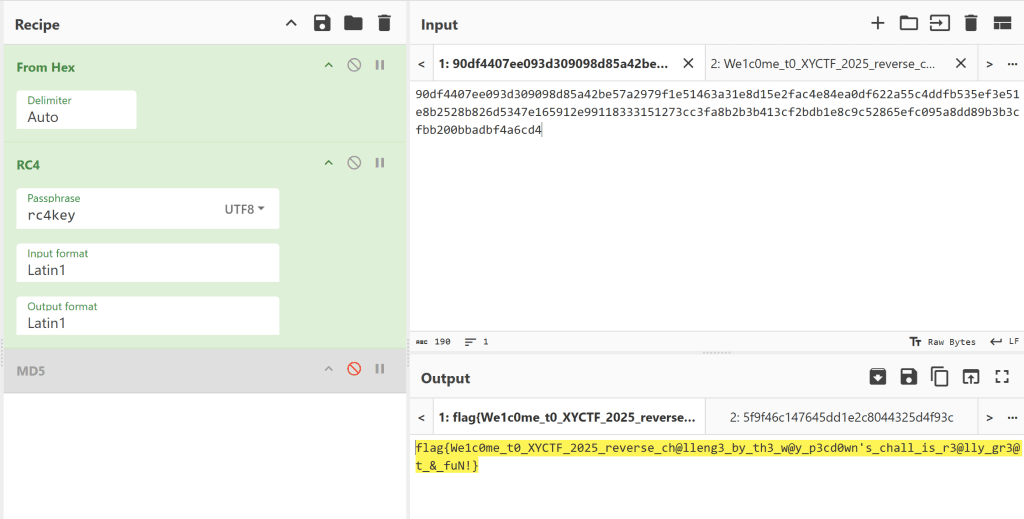
XYCTF{5f9f46c147645dd1e2c8044325d4f93c}
Crypto
Division | Solved – SeanDictioanry
一个简单的MT19937的预测
__import__('os').environ['TERM'] = 'xterm'
from pwn import *
from tqdm import *
from random import *
# context.log_level = 'debug'
addr = "39.106.69.240 20502".split()
io = remote(addr[0], int(addr[1]))
tmp = []
for _ in trange(19968//32):
io.sendlineafter(b": >>>", b"1")
io.sendlineafter(b": >>>", b"1")
tmp += [int(io.recvline().decode().strip().split(" = ")[1])]
def construct_a_row(RNG):
row = []
for _ in range(19968//32):
tmp = RNG.getrandbits(32)
row += list(map(int, bin(tmp)[2:].zfill(32)))
return row
# 构造线性方程组的矩阵
L = []
for i in trange(19968):
state = [0]*624 # MT19937使用624个32位整数作为状态
# 构造一个只有一位为1,其他都为0的序列
temp = "0"*i + "1"*1 + "0"*(19968-1-i)
# 将这个序列分成624段,每段32位,转换为整数
for j in range(624):
state[j] = int(temp[32*j:32*j+32], 2)
RNG = Random()
RNG.setstate((3,tuple(state+[624]),None))
L.append(construct_a_row(RNG))
# 将L转换为GF(2)上的矩阵(二进制域)
L = Matrix(GF(2),L)
print(L.nrows(), L.ncols())
def MT19937_re(state):
try:
# 构造目标向量R
R = []
for i in state:
R += list(map(int, bin(i)[2:].zfill(32)))
R = vector(GF(2), R)
s = L.solve_left(R) # 这里可能会抛出异常
# 将解转换为二进制字符串
init = "".join(list(map(str,s)))
state = []
# 将解重新分割成624个32位整数
for i in range(624):
state.append(int(init[32*i:32*i+32],2))
# 创建新的RNG并设置恢复出的状态
RNG1 = Random()
RNG1.setstate((3,tuple(state+[624]),None))
return RNG1
except Exception as e:
print(f"[-]{e}")
pass
RNG = MT19937_re(tmp)
for _ in range(19968//32):
RNG.getrandbits(32)
a = RNG.getrandbits(11000)
b = RNG.getrandbits(10000)
ans = a//b
io.sendlineafter(b": >>>", b"2")
io.sendlineafter(b": >>>", str(ans).encode())
io.interactive()
# XYCTF{282486a9-5c20-41ad-9fb1-bf508167197e}Complex_signin | Solved – SeanDictionary
首先我用多项式的方法模拟出了复数的计算,即先定义一个模n的多项式环,同时因为$x^2+1=0$即可对这个多项式环取模得到代表复数的一个商环,然后显然能得到复数立方后,和a,b有关的实部和虚部。即可得到两个联立的方程组。
我尝试联立求解,但是一直报错,所以最后没办法尝试用格求解出来。
先对两个多项式输出查看了一下发现是这样的结构
$$\left.\begin{matrix} tmp_1=&p_1a^3&&+p_2ab^2&&+p_3a^2+p_4ab+p_5b^2+p_6a+p_7b+p_8\equiv 0\ mod\ n\\ tmp_2=&&q_1a^2b&&+q_2b^3&+q_3a^2+q_4ab+q_5b^2+q_6a+q_7b+q_8\equiv 0\ mod\ n \end{matrix}\right.$$
$$(k_1,k_2,a^3,a^2b,ab^2,b^3,a^2,ab,b^2,a,b,1) \left(\begin{matrix} n&0&0&0&0&0&0&\cdots&0\\ 0&n&0&0&0&0&0&\cdots&0\\ p_1&0&1&0&0&0&0&\cdots&0\\ 0&q_1&0&1&0&0&0&\cdots&0\\ p_2&0&0&0&1&0&0&\cdots&0\\ 0&q_2&0&0&0&1&0&\cdots&0\\ p_3&q_3&0&0&0&0&1&\cdots&0\\ \vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\ddots&\vdots\\ p_8&q_8&0&0&0&0&0&\cdots&1\\ \end{matrix}\right) =(0,0,a^3,a^2b,ab^2,b^3,a^2,ab,b^2,a,b,1)$$
对格规约找到最后一位是1的就能得到a和b了
from Crypto.Cipher import ChaCha20
import hashlib
n = 24240993137357567658677097076762157882987659874601064738608971893024559525024581362454897599976003248892339463673241756118600994494150721789525924054960470762499808771760690211841936903839232109208099640507210141111314563007924046946402216384360405445595854947145800754365717704762310092558089455516189533635318084532202438477871458797287721022389909953190113597425964395222426700352859740293834121123138183367554858896124509695602915312917886769066254219381427385100688110915129283949340133524365403188753735534290512113201932620106585043122707355381551006014647469884010069878477179147719913280272028376706421104753
mh = [3960604425233637243960750976884707892473356737965752732899783806146911898367312949419828751012380013933993271701949681295313483782313836179989146607655230162315784541236731368582965456428944524621026385297377746108440938677401125816586119588080150103855075450874206012903009942468340296995700270449643148025957527925452034647677446705198250167222150181312718642480834399766134519333316989347221448685711220842032010517045985044813674426104295710015607450682205211098779229647334749706043180512861889295899050427257721209370423421046811102682648967375219936664246584194224745761842962418864084904820764122207293014016, 15053801146135239412812153100772352976861411085516247673065559201085791622602365389885455357620354025972053252939439247746724492130435830816513505615952791448705492885525709421224584364037704802923497222819113629874137050874966691886390837364018702981146413066712287361010611405028353728676772998972695270707666289161746024725705731676511793934556785324668045957177856807914741189938780850108643929261692799397326838812262009873072175627051209104209229233754715491428364039564130435227582042666464866336424773552304555244949976525797616679252470574006820212465924134763386213550360175810288209936288398862565142167552]
C = [5300743174999795329371527870190100703154639960450575575101738225528814331152637733729613419201898994386548816504858409726318742419169717222702404409496156167283354163362729304279553214510160589336672463972767842604886866159600567533436626931810981418193227593758688610512556391129176234307448758534506432755113432411099690991453452199653214054901093242337700880661006486138424743085527911347931571730473582051987520447237586885119205422668971876488684708196255266536680083835972668749902212285032756286424244284136941767752754078598830317271949981378674176685159516777247305970365843616105513456452993199192823148760, 21112179095014976702043514329117175747825140730885731533311755299178008997398851800028751416090265195760178867626233456642594578588007570838933135396672730765007160135908314028300141127837769297682479678972455077606519053977383739500664851033908924293990399261838079993207621314584108891814038236135637105408310569002463379136544773406496600396931819980400197333039720344346032547489037834427091233045574086625061748398991041014394602237400713218611015436866842699640680804906008370869021545517947588322083793581852529192500912579560094015867120212711242523672548392160514345774299568940390940653232489808850407256752]
enc = b'\x9c\xc4n\x8dF\xd9\x9e\xf4\x05\x82!\xde\xfe\x012$\xd0\x8c\xaf\xfb\rEb(\x04)\xa1\xa6\xbaI2J\xd2\xb2\x898\x11\xe6x\xa9\x19\x00pn\xf6rs- \xd2\xd1\xbe\xc7\xf51.\xd4\xd2 \xe7\xc6\xca\xe5\x19\xbe'
R.<x,a,b> = PolynomialRing(Zmod(n))
f = (mh[1]+a)*x + mh[0] + b
g = f**3%(x**2+1)
tmp1 = g//x - C[1]
tmp2 = g%x - C[0]
coffs1 = tmp1.coefficients()
coffs2 = tmp2.coefficients()
ge = [
[n,0,0,0,0,0,0,0,0,0,0,0],
[0,n,0,0,0,0,0,0,0,0,0,0],
[coffs1[0],0,1,0,0,0,0,0,0,0,0,0],
[coffs1[1],0,0,1,0,0,0,0,0,0,0,0],
[0,coffs2[0],0,0,1,0,0,0,0,0,0,0],
[0,coffs2[1],0,0,0,1,0,0,0,0,0,0],
[coffs1[2],coffs2[2],0,0,0,0,1,0,0,0,0,0],
[coffs1[3],coffs2[3],0,0,0,0,0,1,0,0,0,0],
[coffs1[4],coffs2[4],0,0,0,0,0,0,1,0,0,0],
[coffs1[5],coffs2[5],0,0,0,0,0,0,0,1,0,0],
[coffs1[6],coffs2[6],0,0,0,0,0,0,0,0,1,0],
[coffs1[7],coffs2[7],0,0,0,0,0,0,0,0,0,1]
]
Ge = Matrix(ZZ,ge)
L = Ge.LLL()
for i in L:
if i[-1] == 1:
a = i[-3]
b = i[-2]
mh0 = mh[0] + b
mh1 = mh[1] + a
print({ChaCha20.new(key=hashlib.sha256(str(mh0 + mh1).encode()).digest(), nonce=b'Pr3d1ctmyxjj').decrypt(enc)})
# XYCTF{Welcome_to_XYCTF_Now_let_us_together_play_Crypto_challenge}Reed | Sloved – SeanDictionary
这道题目挺有意思的,就是每次用随机数然后处理作为新的种子,也就是说这个随机数生成器更类似于LCG那种输出只与上一次状态有关,因此极易进入循环,于是就可以尝试寻找出一个较短的循环,就能确定a和b的取值范围了
用如下脚本确定出长度为2的循环,初始seed为52331392593937
import random
from tqdm import trange
a = 1145140
b = 19198100
l = 0
while True:
for x in trange(a,b+1):
random.seed(x**2+1)
for _ in range(l):
tmp = random.randint(a,b)
random.seed(tmp**2+1)
if x == random.randint(a,b):
print(x**2+1,l+1)
break
else:
l += 1
continue
break
# 52331392593937 2然后就知道$a,b\in \{17593903,7234044\}$排列组合尝试一下就能解出flag了
import string
table = string.ascii_letters + string.digits
enc = [9363323, 9363323, 4550699, 2946491, 9363323, 4550699, 9572863, 4760239, 19093341, 11177071, 12781279, 12728894, 14333102, 4760239, 15937310, 6312062, 4760239, 7916270, 7916270, 14333102, 12781279, 17593903, 15937310, 7968655, 11177071, 9520478, 14333102, 4707854, 7916270, 9363323, 15727770, 9363323, 15727770, 17331978, 9363323, 10967531]
# 17593903, 7234044
a = 17593903
b = 17593903
for i in enc:
tmp = (i-b)%19198111*pow(a,-1,19198111)%19198111
print(table[tmp], end='')
# XYCTF{114514fixedpointissodangerous1919810}勒索病毒
用NTRU生成密钥然后用国密4对内容进行加密
Choice | Sloved – SeanDictionary
题目给的random库里是这样定义的choice函数
def _randbelow_with_getrandbits(self, n):
"Return a random int in the range [0,n). Defined for n > 0."
getrandbits = self.getrandbits
k = n.bit_length() - 1
r = getrandbits(k) # 0 <= r < 2**k
while r >= n:
r = getrandbits(k)
return r很显然每次choice时生成的下标是一定小于n的,也就是说while循环不会进行,(我还特地去翻了一下我本地的random库py3.9.13版本,对比一下发现,这里就无法判断进行了几次getrandbits
def _randbelow_with_getrandbits(self, n):
"Return a random int in the range [0,n). Returns 0 if n==0."
if not n:
return 0
getrandbits = self.getrandbits
k = n.bit_length() # don't use (n-1) here because n can be 1
r = getrandbits(k) # 0 <= r < 2**k
while r >= n:
r = getrandbits(k)
return r然后就能从给出的choice生成的列表得到每次输出的随机数然后逆向即可。
但是这里有个问题,异或时候也生成了随机数,但是不知道是多少位的,但可以确定这里的位数一定大于等于enc的位数,然后爆破一下即可
from Crypto.Util.number import *
from tqdm import trange
from random import *
for i in range(5):
enc = 5042764371819053176884777909105310461303359296255297
r = [224, 55, 218, 253, 150, 84, 208, 134, 18, 177, 244, 54, 122, 193, 249, 5, 121, 80, 230, 21, 236, 33, 226, 3, 120, 141, 212, 33, 69, 195, 78, 112, 0, 62, 64, 197, 10, 224, 64, 191, 17, 112, 196, 143, 209, 92, 10, 198, 174, 181, 96, 118, 175, 145, 111, 41, 113, 206, 137, 37, 56, 227, 252, 84, 18, 145, 81, 124, 202, 14, 255, 144, 200, 13, 230, 218, 208, 210, 222, 101, 211, 114, 222, 12, 190, 226, 62, 118, 87, 152, 118, 245, 196, 4, 92, 251, 238, 142, 114, 13, 113, 247, 171, 8, 138, 20, 169, 192, 221, 223, 60, 56, 188, 70, 184, 202, 195, 246, 71, 235, 152, 255, 73, 128, 140, 159, 119, 79, 1, 223, 239, 242, 60, 228, 205, 90, 210, 5, 165, 35, 176, 75, 21, 182, 220, 212, 240, 212, 77, 124, 52, 140, 85, 200, 207, 31, 177, 82, 76, 152, 128, 124, 205, 216, 252, 34, 27, 198, 186, 61, 161, 192, 158, 226, 40, 127, 69, 162, 24, 46, 208, 183, 99, 165, 1, 221, 184, 40, 147, 136, 236, 245, 228, 197, 86, 15, 201, 95, 115, 18, 131, 79, 86, 12, 122, 63, 200, 192, 244, 205, 229, 36, 86, 217, 249, 170, 5, 134, 99, 33, 214, 10, 120, 105, 233, 115, 230, 114, 105, 84, 39, 167, 18, 10, 77, 236, 104, 225, 196, 181, 105, 180, 159, 24, 4, 147, 131, 143, 64, 201, 212, 175, 203, 200, 19, 99, 24, 112, 180, 75, 222, 204, 204, 13, 210, 165, 135, 175, 132, 205, 247, 28, 178, 76, 240, 196, 240, 121, 132, 21, 8, 45, 203, 143, 206, 6, 11, 51, 47, 87, 88, 35, 63, 168, 251, 11, 254, 11, 46, 72, 210, 230, 184, 114, 88, 194, 99, 229, 144, 1, 226, 44, 133, 10, 42, 234, 112, 100, 248, 247, 66, 221, 72, 229, 236, 4, 65, 203, 65, 61, 23, 181, 190, 87, 1, 76, 113, 48, 178, 42, 175, 49, 78, 159, 104, 229, 213, 223, 13, 249, 216, 60, 144, 203, 156, 23, 129, 148, 87, 37, 79, 227, 141, 202, 210, 245, 236, 121, 129, 78, 7, 121, 42, 82, 184, 222, 96, 100, 189, 62, 102, 176, 198, 1, 153, 242, 23, 191, 197, 176, 115, 206, 122, 50, 104, 70, 170, 29, 52, 189, 157, 99, 82, 187, 201, 78, 25, 75, 126, 118, 160, 250, 53, 112, 143, 161, 251, 221, 44, 255, 232, 115, 182, 77, 31, 217, 228, 97, 112, 236, 21, 160, 127, 9, 220, 22, 97, 159, 239, 25, 140, 206, 210, 148, 105, 184, 41, 56, 92, 141, 3, 200, 165, 14, 161, 219, 177, 40, 189, 75, 48, 146, 130, 151, 100, 144, 239, 22, 19, 246, 166, 231, 228, 68, 254, 16, 99, 95, 32, 177, 216, 170, 125, 211, 100, 142, 251, 16, 64, 83, 161, 184, 242, 248, 239, 141, 171, 135, 48, 20, 34, 250, 13, 70, 236, 172, 22, 241, 171, 25, 18, 204, 36, 248, 253, 203, 138, 10, 130, 249, 15, 157, 244, 154, 41, 4, 231, 64, 20, 212, 126, 160, 48, 154, 171, 250, 199, 113, 32, 186, 126, 217, 3, 236, 115, 37, 174, 75, 222, 125, 55, 86, 65, 96, 56, 254, 226, 213, 244, 36, 199, 164, 160, 126, 191, 29, 50, 135, 234, 165, 122, 132, 68, 133, 129, 0, 220, 72, 87, 172, 93, 15, 131, 37, 119, 240, 43, 239, 105, 45, 244, 6, 34, 111, 151, 144, 54, 46, 159, 6, 5, 160, 32, 4, 180, 246, 39, 220, 85, 209, 145, 41, 88, 137, 110, 101, 113, 115, 204, 11, 53, 152, 177, 240, 193, 220, 136, 84, 221, 12, 43, 74, 122, 251, 236, 53, 175, 36, 46, 246, 181, 137, 246, 53, 189, 171, 240, 104, 8, 126, 56, 122, 245, 155, 130, 31, 16, 20, 212, 147, 33, 165, 82, 117, 244, 167, 235, 115, 244, 94, 173, 195, 34, 36, 33, 218, 39, 13, 90, 196, 172, 207, 105, 73, 255, 187, 221, 162, 242, 186, 122, 140, 241, 120, 98, 44, 81, 172, 201, 150, 238, 111, 147, 24, 214, 192, 125, 102, 157, 53, 219, 172, 123, 218, 222, 71, 138, 117, 188, 32, 104, 10, 188, 118, 58, 254, 36, 104, 212, 76, 209, 15, 6, 33, 149, 15, 225, 76, 8, 157, 48, 70, 127, 19, 126, 77, 216, 133, 132, 30, 33, 113, 117, 134, 238, 57, 20, 121, 26, 184, 229, 202, 90, 28, 42, 230, 42, 159, 19, 191, 162, 205, 241, 67, 177, 216, 191, 164, 146, 90, 228, 232, 149, 163, 135, 130, 193, 196, 178, 215, 216, 155, 238, 20, 36, 196, 153, 207, 177, 149, 40, 172, 139, 12, 134, 142, 154, 225, 179, 95, 248, 190, 8, 154, 246, 229, 102, 121, 197, 116, 135, 163, 128, 109, 112, 114, 143, 164, 134, 233, 45, 244, 22, 141, 211, 214, 122, 14, 93, 49, 251, 85, 95, 95, 191, 210, 245, 181, 142, 125, 110, 33, 195, 150, 197, 173, 86, 50, 127, 187, 129, 67, 119, 58, 134, 119, 36, 151, 136, 122, 157, 22, 171, 195, 48, 178, 232, 228, 177, 6, 124, 50, 163, 161, 32, 49, 197, 157, 188, 86, 208, 226, 208, 63, 173, 21, 192, 148, 194, 208, 251, 95, 117, 34, 116, 217, 130, 150, 97, 206, 101, 201, 88, 137, 163, 90, 104, 129, 4, 191, 99, 50, 115, 8, 145, 116, 250, 180, 193, 229, 128, 92, 55, 26, 6, 154, 68, 0, 66, 77, 126, 192, 170, 218, 252, 127, 192, 29, 107, 152, 231, 190, 202, 130, 116, 229, 193, 63, 13, 48, 220, 238, 126, 74, 232, 19, 242, 71, 159, 9, 196, 187, 111, 243, 81, 244, 193, 95, 166, 85, 22, 240, 32, 1, 114, 11, 64, 114, 149, 217, 207, 194, 1, 33, 245, 14, 101, 119, 32, 233, 214, 139, 71, 103, 125, 54, 17, 86, 140, 132, 221, 45, 227, 136, 203, 156, 223, 73, 43, 82, 190, 119, 22, 14, 115, 0, 192, 105, 147, 210, 146, 47, 89, 210, 18, 225, 126, 210, 240, 55, 219, 247, 106, 190, 50, 35, 13, 255, 236, 253, 82, 244, 117, 139, 1, 72, 182, 19, 170, 173, 59, 175, 10, 95, 66, 253, 178, 139, 45, 5, 24, 59, 9, 222, 58, 46, 79, 48, 39, 175, 196, 249, 249, 70, 126, 118, 69, 165, 155, 119, 67, 221, 20, 133, 16, 99, 41, 132, 11, 12, 35, 70, 87, 43, 197, 103, 33, 201, 3, 195, 142, 128, 135, 121, 26, 185, 2, 73, 235, 70, 219, 49, 227, 133, 241, 34, 6, 9, 109, 66, 50, 177, 114, 119, 101, 91, 144, 41, 246, 40, 81, 113, 203, 226, 87, 8, 0, 73, 212, 5, 95, 112, 230, 4, 28, 206, 93, 252, 30, 195, 197, 226, 165, 120, 3, 124, 169, 66, 227, 113, 55, 101, 135, 141, 71, 84, 202, 19, 145, 25, 92, 50, 80, 53, 63, 85, 184, 196, 93, 254, 47, 252, 182, 150, 115, 20, 181, 178, 87, 162, 50, 190, 228, 125, 240, 134, 10, 142, 173, 206, 250, 49, 186, 201, 118, 146, 246, 244, 199, 9, 55, 253, 123, 103, 200, 206, 79, 168, 216, 99, 192, 191, 236, 214, 248, 111, 115, 74, 155, 165, 150, 40, 86, 224, 240, 133, 69, 34, 52, 13, 63, 61, 116, 182, 144, 177, 101, 164, 77, 217, 65, 218, 150, 142, 249, 165, 160, 220, 120, 25, 36, 157, 134, 223, 11, 46, 121, 75, 182, 126, 104, 91, 204, 45, 49, 175, 10, 48, 83, 150, 96, 244, 10, 149, 76, 124, 189, 149, 200, 252, 175, 124, 146, 126, 230, 70, 194, 243, 63, 204, 224, 115, 140, 115, 110, 86, 22, 193, 5, 11, 18, 177, 159, 94, 160, 38, 188, 139, 89, 1, 200, 163, 138, 8, 140, 169, 54, 29, 225, 22, 5, 99, 144, 247, 239, 106, 77, 29, 141, 206, 89, 236, 4, 32, 104, 115, 206, 204, 15, 100, 66, 199, 15, 89, 24, 246, 99, 224, 207, 7, 205, 142, 203, 28, 87, 16, 110, 93, 72, 73, 206, 48, 59, 170, 152, 224, 2, 74, 9, 125, 140, 82, 206, 159, 0, 117, 237, 252, 47, 200, 75, 133, 68, 239, 109, 169, 25, 168, 202, 240, 5, 67, 125, 173, 233, 6, 148, 38, 182, 13, 141, 149, 39, 119, 189, 122, 49, 173, 153, 78, 103, 211, 65, 224, 52, 10, 35, 233, 88, 66, 43, 120, 255, 71, 169, 215, 250, 218, 205, 163, 164, 226, 46, 178, 25, 88, 59, 98, 199, 167, 134, 244, 167, 210, 20, 246, 159, 163, 252, 114, 5, 168, 52, 47, 177, 159, 255, 236, 166, 49, 36, 61, 10, 130, 135, 220, 101, 202, 69, 150, 100, 217, 98, 203, 217, 166, 33, 169, 203, 230, 194, 224, 15, 249, 205, 52, 41, 124, 191, 223, 148, 251, 147, 133, 85, 149, 214, 198, 5, 134, 91, 201, 191, 204, 152, 240, 37, 34, 236, 211, 182, 142, 207, 1, 188, 67, 87, 222, 220, 7, 78, 49, 129, 236, 98, 120, 217, 204, 77, 106, 89, 250, 182, 15, 18, 27, 143, 13, 27, 61, 223, 213, 196, 190, 24, 35, 104, 100, 220, 60, 194, 174, 169, 20, 167, 75, 162, 26, 253, 213, 59, 219, 187, 253, 160, 249, 61, 122, 113, 223, 55, 57, 198, 53, 138, 94, 154, 18, 132, 233, 183, 71, 7, 22, 50, 196, 181, 202, 103, 86, 31, 119, 83, 130, 165, 242, 170, 31, 35, 175, 117, 95, 89, 247, 221, 186, 47, 236, 241, 77, 194, 111, 148, 45, 101, 88, 41, 0, 33, 139, 15, 127, 156, 72, 234, 217, 170, 218, 216, 31, 4, 73, 150, 78, 49, 178, 13, 178, 46, 102, 93, 184, 110, 205, 132, 190, 43, 87, 194, 35, 188, 166, 9, 97, 184, 202, 113, 45, 150, 62, 106, 108, 19, 162, 85, 212, 188, 131, 38, 67, 23, 136, 208, 87, 63, 69, 6, 209, 242, 45, 13, 228, 14, 233, 8, 71, 43, 51, 89, 46, 195, 101, 132, 254, 154, 183, 220, 115, 221, 255, 174, 150, 65, 141, 176, 57, 144, 16, 115, 252, 144, 139, 52, 205, 224, 75, 190, 192, 2, 231, 30, 238, 149, 22, 200, 137, 244, 239, 185, 212, 145, 230, 200, 8, 249, 109, 26, 226, 195, 133, 140, 103, 50, 230, 180, 47, 196, 226, 105, 13, 239, 135, 20, 214, 152, 211, 208, 81, 213, 48, 187, 232, 77, 139, 16, 79, 204, 216, 56, 41, 41, 58, 192, 245, 1, 104, 85, 42, 107, 94, 142, 12, 247, 90, 254, 116, 72, 193, 219, 54, 247, 5, 28, 60, 140, 10, 185, 86, 148, 101, 198, 96, 181, 245, 61, 25, 186, 29, 57, 176, 188, 9, 239, 93, 198, 110, 248, 23, 87, 193, 161, 107, 40, 38, 186, 205, 148, 197, 127, 144, 69, 19, 47, 132, 82, 23, 170, 83, 224, 235, 49, 190, 44, 145, 65, 66, 141, 78, 1, 254, 24, 157, 7, 23, 227, 28, 81, 176, 22, 92, 139, 188, 48, 183, 229, 139, 205, 174, 131, 189, 241, 21, 146, 204, 58, 249, 167, 217, 174, 43, 41, 56, 181, 212, 42, 188, 6, 117, 93, 178, 160, 129, 15, 76, 150, 207, 245, 227, 247, 130, 171, 114, 204, 101, 176, 55, 43, 138, 149, 90, 124, 45, 96, 181, 221, 16, 121, 210, 51, 210, 164, 68, 64, 154, 167, 91, 69, 35, 153, 212, 10, 125, 235, 203, 166, 145, 9, 174, 86, 65, 70, 112, 194, 140, 92, 170, 49, 191, 157, 218, 199, 152, 151, 247, 208, 182, 209, 34, 245, 5, 173, 105, 175, 159, 71, 251, 198, 246, 214, 99, 58, 70, 154, 52, 39, 88, 149, 179, 202, 86, 240, 108, 200, 83, 250, 62, 213, 113, 138, 73, 106, 141, 192, 204, 90, 251, 208, 28, 124, 30, 134, 119, 144, 68, 23, 204, 181, 186, 76, 156, 71, 8, 104, 186, 87, 221, 134, 122, 72, 244, 203, 121, 181, 65, 90, 185, 131, 230, 133, 54, 158, 186, 168, 201, 178, 155, 172, 164, 22, 130, 111, 90, 209, 2, 167, 23, 176, 63, 139, 89, 63, 15, 238, 110, 204, 85, 36, 127, 68, 240, 177, 31, 2, 81, 147, 205, 192, 214, 173, 103, 130, 10, 100, 232, 125, 216, 163, 209, 171, 168, 243, 145, 6, 170, 41, 142, 250, 145, 57, 139, 224, 221, 189, 48, 141, 232, 146, 92, 216, 154, 126, 223, 8, 90, 82, 138, 221, 240, 223, 87, 209, 165, 17, 52, 154, 91, 12, 121, 212, 238, 46, 215, 217, 147, 136, 139, 251, 91, 39, 188, 244, 251, 52, 110, 22, 126, 200, 231, 153, 103, 203, 120, 219, 118, 172, 53, 141, 203, 75, 163, 150, 194, 27, 208, 9, 186, 6, 85, 46, 243, 135, 66, 40, 79, 206, 250, 20, 85, 123, 35, 164, 44, 85, 104, 66, 51, 177, 125, 189, 165, 226, 13, 75, 78, 225, 252, 226, 138, 81, 171, 172, 175, 122, 145, 68, 254, 37, 153, 39, 113, 237, 232, 220, 80, 193, 181, 21, 197, 186, 56, 202, 239, 213, 135, 41, 6, 85, 54, 135, 214, 95, 102, 23, 192, 153, 235, 110, 26, 14, 84, 220, 142, 236, 192, 8, 117, 205, 249, 92, 148, 149, 77, 235, 205, 232, 21, 48, 14, 84, 187, 124, 218, 166, 155, 183, 62, 10, 123, 53, 63, 79, 101, 193, 3, 61, 29, 39, 99, 22, 197, 75, 10, 165, 44, 215, 210, 181, 74, 235, 200, 247, 158, 187, 200, 102, 22, 150, 73, 42, 131, 28, 17, 180, 133, 205, 23, 228, 226, 219, 175, 207, 81, 53, 141, 114, 140, 59, 218, 169, 7, 219, 139, 75, 210, 97, 236, 157, 21, 109, 195, 128, 54, 5, 55, 217, 127, 49, 62, 59, 101, 95, 86, 255, 22, 186, 94, 151, 114, 93, 19, 198, 159, 174, 142, 132, 195, 157, 206, 161, 107, 255, 106, 196, 250, 191, 86, 221, 196, 36, 29, 37, 50, 224, 42, 20, 89, 212, 252, 191, 157, 237, 10, 157, 80, 42, 234, 180, 1, 183, 186, 239, 129, 14, 125, 114, 66, 203, 120, 114, 37, 214, 37, 73, 153, 182, 165, 87, 177, 75, 220, 210, 105, 154, 149, 114, 13, 202, 128, 55, 128, 96, 158, 150, 57, 86, 106, 127, 160, 57, 80, 255, 107, 241, 95, 121, 14, 110, 160, 119, 211, 150, 156, 185, 158, 221, 110, 76, 255, 119, 15, 245, 1, 238, 139, 100, 250, 220, 147, 193, 51, 144, 123, 139, 13, 26, 158, 95, 148, 251, 82, 227, 119, 92, 132, 219, 248, 239, 217, 101, 88, 121, 10, 148, 203, 156, 156]
bits = int(enc).bit_length()+i
def construct_a_row(RNG):
row = []
RNG.getrandbits(bits)
for _ in range(19968//8):
tmp = RNG.getrandbits(8)
row += list(map(int, bin(tmp)[2:].zfill(8)))
return row
# 构造线性方程组的矩阵
L = []
for i in trange(19968):
state = [0]*624 # MT19937使用624个32位整数作为状态
# 构造一个只有一位为1,其他都为0的序列
temp = "0"*i + "1"*1 + "0"*(19968-1-i)
# 将这个序列分成624段,每段32位,转换为整数
for j in range(624):
state[j] = int(temp[32*j:32*j+32], 2)
RNG = Random()
RNG.setstate((3,tuple(state+[624]),None))
L.append(construct_a_row(RNG))
# 将L转换为GF(2)上的矩阵(二进制域)
L = Matrix(GF(2),L)
print(L.nrows(), L.ncols())
def MT19937_re(state):
try:
# 构造目标向量R
R = []
for i in state:
R += list(map(int, bin(255-i)[2:].zfill(8)))
R = vector(GF(2), R)
s = L.solve_left(R) # 这里可能会抛出异常
# 将解转换为二进制字符串
init = "".join(list(map(str,s)))
state = []
# 将解重新分割成624个32位整数
for i in range(624):
state.append(int(init[32*i:32*i+32],2))
# 创建新的RNG并设置恢复出的状态
RNG1 = Random()
RNG1.setstate((3,tuple(state+[624]),None))
return RNG1
except Exception as e:
print(f"[-]{e}")
pass
RNG = MT19937_re(r)
tmp = RNG.getrandbits(bits)
print(long_to_bytes(int(enc ^^ tmp)))
# × 0 b'\x07>_0h_51mple_r@nd0m___'
# × 1 b'\x19\xf3_0h_51mple_r@nd0m___'
# × 2 b'$h_0h_51mple_r@nd0m___'
# √ 3 b'___0h_51mple_r@nd0m___'
# × 4 b'\xa90_0h_51mple_r@nd0m___'XYCTF{___0h_51mple_r@nd0m___}
复复复复数 | 复现 -SeanDictionary
这里涉及到了四元数的数学概念
魔改了一下四元数的定义,新增了矩阵表示
套用了一下四元数的矩阵表示,然后用solve_right就可以直接解矩阵了
后面是不互质的做法,需要涉及到开方,不过这个exp为什么不用开方就能做出来呢,因为实际上这道题对应m的元素阶是小于群阶的,然而我们一直用群阶$p^4-1$来寻找d此时自然会要用到CRT来合并。但是对于题目的数据用$\frac{p^4-1}{3}$作为元素阶也是可以的,因此可以直接用这个互质的阶来计算私钥,然后求解RSA即可
from Crypto.Util.number import *
class ComComplex:
def __init__(self, value=[0,0,0,0]):
if type(value) == str:
self.value = [int(i[:-1]) if i[-1] in 'ijk' else int(i) for i in value.split('+')]
self.matrix_init()
elif type(value) == list:
self.value = value
self.matrix_init()
else:
self.matrix = Matrix(ZZ,value)
self.value = [self.matrix[0][0], self.matrix[1][0], self.matrix[2][0], self.matrix[3][0]]
def matrix_init(self):
a,b,c,d = self.value
self.matrix = Matrix(ZZ,[
[a, -b, -c, -d],
[b, a, -d, c],
[c, d, a, -b],
[d, -c, b, a]
])
def __str__(self):
s = str(self.value[0])
for k,i in enumerate(self.value[1:]):
if i >= 0:
s += '+'
s += str(i) +'ijk'[k]
return s
def __add__(self,x):
return ComComplex([i+j for i,j in zip(self.value,x.value)])
def __mul__(self,x):
a = self.value[0]*x.value[0]-self.value[1]*x.value[1]-self.value[2]*x.value[2]-self.value[3]*x.value[3]
b = self.value[0]*x.value[1]+self.value[1]*x.value[0]+self.value[2]*x.value[3]-self.value[3]*x.value[2]
c = self.value[0]*x.value[2]-self.value[1]*x.value[3]+self.value[2]*x.value[0]+self.value[3]*x.value[1]
d = self.value[0]*x.value[3]+self.value[1]*x.value[2]-self.value[2]*x.value[1]+self.value[3]*x.value[0]
return ComComplex([a,b,c,d])
def __mod__(self,x):
return ComComplex([i % x for i in self.value])
def __pow__(self, x, n=None):
tmp = ComComplex(self.value)
a = ComComplex([1,0,0,0])
while x:
if x & 1:
a *= tmp
tmp *= tmp
if n:
a %= n
tmp %= n
x >>= 1
return a
hint = "375413371936+452903063925i+418564633198j+452841062207k"
gift = "8123312244520119413231609191866976836916616973013918670932199631084038015924368317077919454611785179950870055560079987034735836668109705445946887481003729+20508867471664499348708768798854433383217801696267611753941328714877299161068885700412171i+22802458968832151777449744120185122420871929971817937643641589637402679927558503881707868j+40224499597522456323122179021760594618350780974297095023316834212332206526399536884102863k"
c = "212391106108596254648968182832931369624606731443797421732310126161911908195602305474921714075911012622738456373731638115041135121458776339519085497285769160263024788009541257401354037620169924991531279387552806754098200127027800103+24398526281840329222660628769015610312084745844610670698920371305353888694519135578269023873988641161449924124665731242993290561874625654977013162008430854786349580090169988458393820787665342793716311005178101342140536536153873825i+45426319565874516841189981758358042952736832934179778483602503215353130229731883231784466068253520728052302138781204883495827539943655851877172681021818282251414044916889460602783324944030929987991059211909160860125047647337380125j+96704582331728201332157222706704482771142627223521415975953255983058954606417974983056516338287792260492498273014507582247155218239742778886055575426154960475637748339582574453542182586573424942835640846567809581805953259331957385k"
P = 8123312244520119413231609191866976836916616973013918670932199631182724263362174895104545305364960781233690810077210539091362134310623408173268475389315109
n = 408713495380933615345467409596399184629824932933932227692519320046890365817329617301604051766392980053993030281090124694858194866782889226223493799859404283664530068697313752856923001112586828837146686963124061670340088332769524367
e = 65547
hint, gift, c = map(ComComplex, [hint, gift, c])
_, p, q, r = ComComplex(matrix(Zmod(P), hint.matrix).solve_right(matrix(Zmod(P), gift.matrix))).value
assert n == p*q*r
m = pow(c, int(pow(e,-1,(p**4-1)*(q**4-1)*(r**4-1)//27)), n)
print(m)
for i in m.value:
print(long_to_bytes(int(i)).decode(), end='')
# flag{Quaternion_15_ComComComComplexXXX!!!?}后面有空补一下如何计算根号的做法
Misc
XGCTF | Solved – Yolo
不做评价了吧
先是找到LamentXU在西瓜杯出的题目,在ctfshow中有西瓜杯的归档,一眼就知道和污染链有关系,不多说了,然后在这位师傅的博客中找的关于polluted的博客https://dragonkeeep.top/category/CISCN%E5%8D%8E%E4%B8%9C%E5%8D%97WEB-Polluted/?highlight=pol
然后文章内容和评论我都找过,发现没啥用,然后我F12查了源码,找到串有zmxh的base64编码,解码后就是flag
flag{1t_I3_t3E_s@Me_ChAl1eNge_aT_a1L_P1e@se_fOrg1ve_Me}
会飞的雷克萨斯 | Sloved – SeanDictioanry
搜一下店名就能定位了,然后标注中铁店,意味这里是中铁城市中心的沿街商铺
flag{四川省内江市资中县春岚北路中铁城市中心内}
签个到吧 | Solved – Yolo,Spreng
注意到代码有一定规律,于是这样分行。
>+++++++++++++++++[<++++++>-+-+-+-]<[-]
>++++++++++++[<+++++++++>-+-+-+-]<[-]
>+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++[<+>-+-+-+-]<[-]
>+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++[<+>-+-+-+-]<[-]
>+++++++++++++++++++++++++++++++++++++++++[<+++>-+-+-+-]<[-]
>+++++++++++++++++++++++++++++[<+++>-+-+-+-]<[-]
>+++++++++++++++++[<+++>-+-+-+-]<[-]
>++++++++++++[<+++++++++>-+-+-+-]<[-]
>+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++[<+>-+-+-+-]<[-]
>++++++++[<++++++>-+-+-+-]<[-]
>+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++[<+>-+-+-+-]<[-]
>+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++[<+>-+-+-+-]<[-]
>+++++++++++++++++++[<+++++>-+-+-+-]<[-]
>+++++++++++++++++++++++++++++[<++++>-+-+-+-]<[-]
>++++++++[<++++++>-+-+-+-]<[-]
>+++++++++++++++++++[<+++++>-+-+-+-]<[-]
>+++++++++++[<++++++++>-+-+-+-]<[-]
>+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++[<+>-+-+-+-]<[-]
>+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++[<+>-+-+-+-]<[-]
>++++++++++++[<+++++++>-+-+-+-]<[-]
>++++++++++[<+++++++>-+-+-+-]<[-]
>+++++++++++++++++++[<+++++>-+-+-+-]<[-]
>++++++++++[<+++++>-+-+-+-]<[-]
>++++++++[<++++++>-+-+-+-]<[-]
>++++++++++[<+++++>-+-+-+-]<[-]
>+++++++++++++++++++++++++++++++++++++++++++++++++++++[<+>-+-+-+-]<[-]
>+++++++++++++++++++[<+++++>-+-+-+-]<[-]
>+++++++++++++++++++++++[<+++>-+-+-+-]<[-]
>+++++++++++[<++++++++++>-+-+-+-]<[-]
>+++++++++++++++++++++++++++++++++++++++++++++++++++++[<++>-+-+-+-]<[-]
>++++++++[<++++++>-+-+-+-]<[-]
>+++++++++++[<+++++>-+-+-+-]<[-]
>+++++++++++++++++++[<+++++>-+-+-+-]<[-]
>+++++++[<+++++++>-+-+-+-]<[-]
>+++++++++++++++++++++++++++++[<++++>-+-+-+-]<[-]
>+++++++++++[<+++>-+-+-+-]<[-]
>+++++++++++++++++++++++++[<+++++>-+-+-+-]<[-]每行的格式相似,例如这样一句,用python翻译一下。这一行计算的值就是4*6=24,但被<[-]给清零了,所以直接运行没有回显。
# >++++[<++++++>-+-+-+-]<[-]
data = [0, 0]
ptr = 0
ptr += 1
data[ptr] += 4
while data[ptr] != 0:
ptr -= 1
data[ptr] += 6
ptr += 1
data[ptr] -= 1
print(data) # [24, 0]
ptr -= 1
while data[ptr] != 0:
data[ptr] -= 1
print(data) # [0, 0]
我们可以写脚本,把每行的乘积给算出来再转换成字符。或者简单点,在[-]前加一个.来输出。