在几何中，对于一条曲线如果他是奇异的，那么该曲线至少有一个奇异点满足该点处的偏导数同时为零（该点处切线不定）。若一个曲线存在奇异点那么这个曲线一定是奇异曲线。

在ECC中对于常见的 Weierstrass 曲线可以用判别式判定该曲线是否奇异

$$ \Delta=-16(4a^3+27b^2) $$

当判别式为0时，该曲线为奇异曲线。当判别式不为0时，该曲线为非奇异曲线。奇异曲线在ECC中是应该绝对不允许使用的。下属奇异曲线均指椭圆曲线中的奇异曲线。

对于奇异曲线，有两种类型分别是尖点曲线和自交点曲线。有这样的判断方式

对 $x^3+ax+b$ 进行因式分解，若有一个三重根则为尖点曲线，若有一个二重根则为自交点曲线。

尖点曲线

$$ y^2=x^3 $$

该曲线就是尖点曲线，可以注意到这个曲线在原点处有一个奇异点，也可以称之为尖点cusp

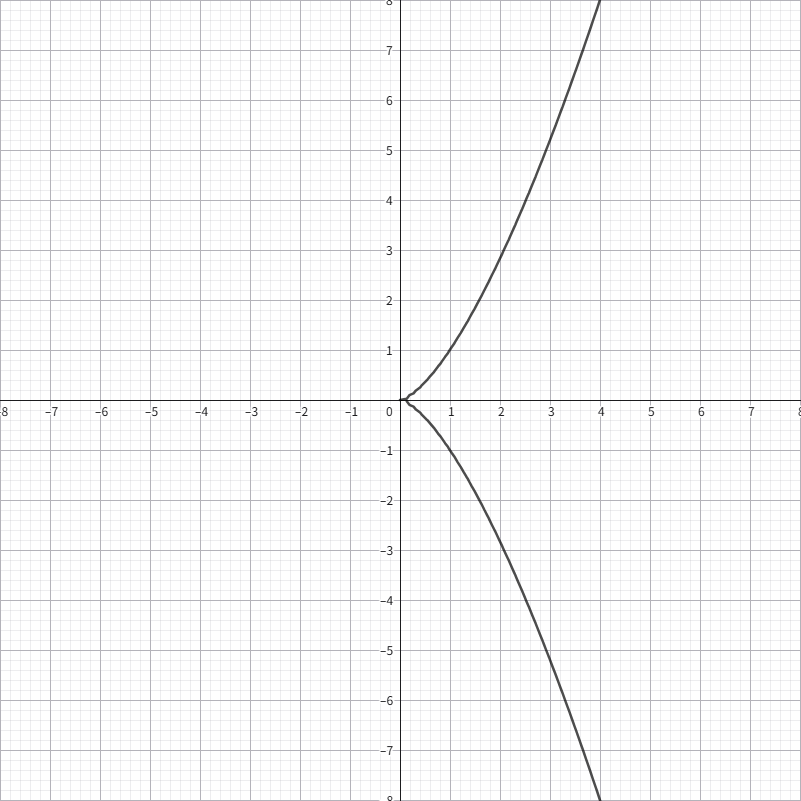
将原式转化为参数方程，并令$P=(t_1^2,t_1^3),Q=(t_2^2,t_2^3)$利用椭圆曲线上的加法原理得到$(P+Q).x=k^2-t_1^2-t_2^2$带入曲线方程化简得到$(P+Q).x=\frac{t_1^2t_2^2}{{t_1+t_2}^2}$，于是就能得到点加运算后的值$P+Q=R=(\frac{t_1t_2}{t_1+t_2}^2,\frac{t_1t_2}{t_1+t_2}^3)$，于是就可以构造处这样的映射关系$f(x,y)\to \frac{x}{y}$将原曲线上的加法运算同构映射到整数上的加法运算，有如下的特性

$$ \begin{align} &f(P+Q)=f(P)+f(Q)\\ &f(xP)=xf(P) \end{align} $$

于是就可以将困难的ECDLP问题转化到有限域上的乘法问题，就能快速解决了。

自交点曲线

$$ y^2=x^3-3x+2 $$

该曲线就是自交点曲线，可以注意到这个曲线在(1,0)处有一个奇异点，也可以称之为自交点node

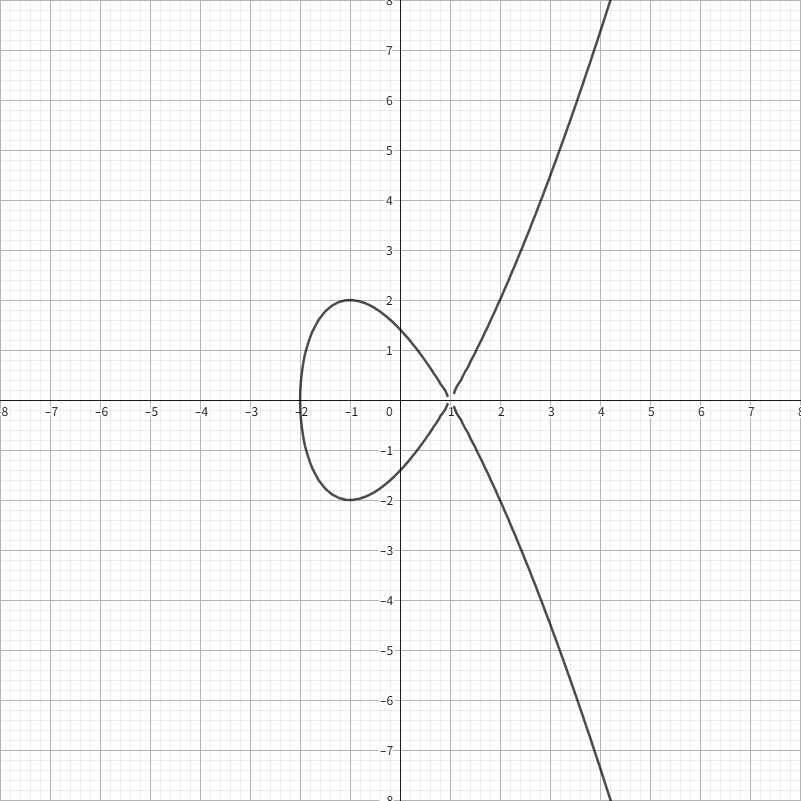
和尖点曲线一样，我们试图对自交点曲线进行类似的同构映射以便将ECDLP转化。

首先可以通过图像的平移，将曲线$y^2=x^3+ax+b=(x+m)^2(x+n)$平移到自交点为原点处，同时受限于自交点自身的性质，所以此时的曲线方程一定是形如$y^2=x^3+Ax^2$，容易得到$A=n-m$，然后考虑一条过奇异点的直线$y=kx$，于是就可以利用k写出曲线的参数方程

$$ \left\{\begin{align} &y=kx\\ &y^2=x^3+Ax^2 \end{align}\right. \Rightarrow x=A-k^2 $$

得到奇异点处的两条切线斜率为$\pm \sqrt{A}$，然后构造这样的映射关系，将椭圆曲线上的加法运算同构映射到整数上的幂运算。

$$ f(x,y)\to \frac{y-\sqrt{A}(x+m)}{y+\sqrt{A}(x+m)} $$

该映射满足以下关系

$$ \begin{align} &f(P+Q)=f(P)\cdot f(Q)\\ &f(xP)={f(P)}^x \end{align} $$

最终将ECDLP问题转化为DLP问题