ECC
|
|
424
|
3
|
CTF

椭圆曲线密码学（ECC）是一种基于椭圆曲线数学结构的公钥密码学方法。ECC 的安全性基于椭圆曲线离散对数问题（ECDLP）

椭圆曲线

Weierstrass 曲线

Weierstrass 曲线通常是一个在平面上由关于 $x$ 和 $y$ 的方程定义的曲线，形式通常为

$$ y^2 = x^3 + ax + b $$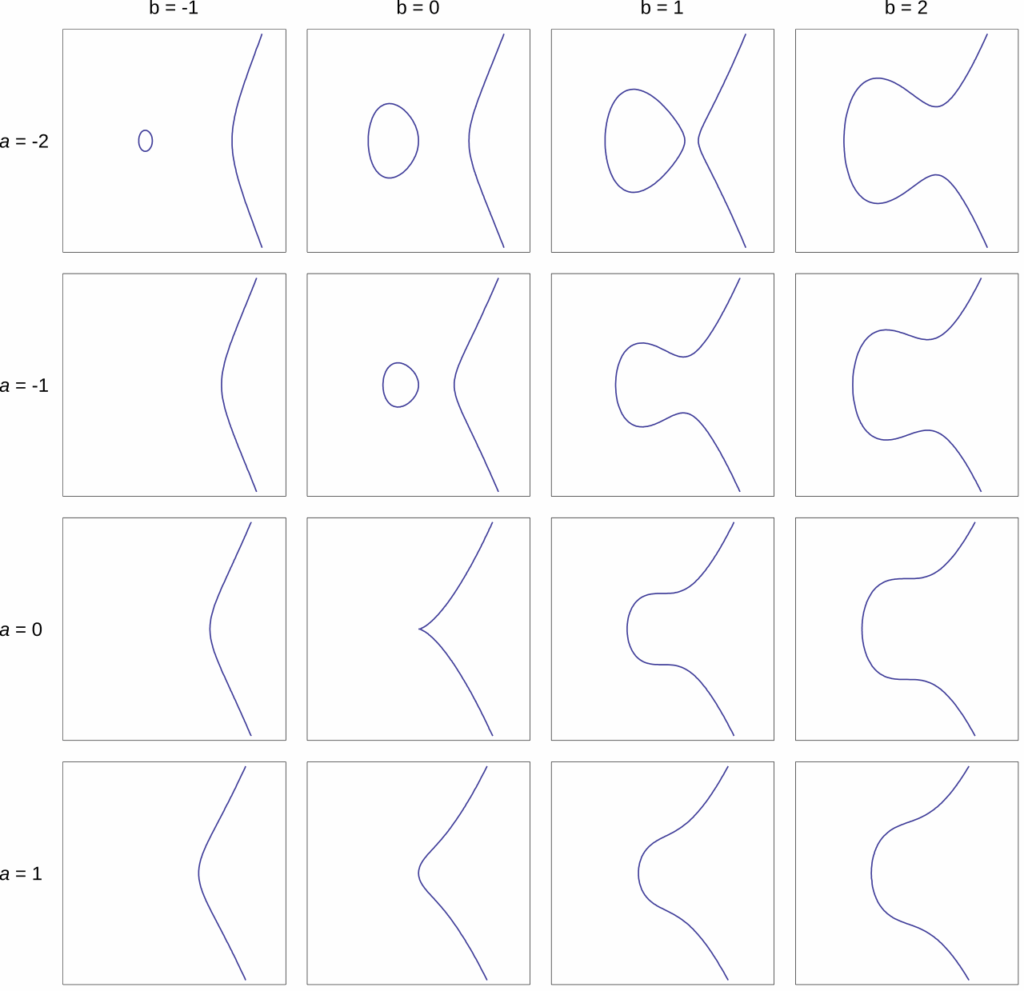

这样形式的曲线，也通常称为 Weierstrass 曲线。

当这个方程表示的曲线是一条连续的曲线时，当且仅当判别式

$$ \Delta=-16(4a^3+27b^2)\ne 0 $$

了能符合密码学的使用，需要对其变换使得能够在有限群上进行运算，先选出大素数$p$，然后可以定义出在椭圆曲线上的点的加法运算。先定义 0 点为椭圆曲线上的无穷远点，记作 $\mathcal{O}$。对于两个点 $P$ 和 $Q$，可以通过以下步骤计算它们的和 $R = P + Q$：

  1. 连接 $P$ 和 $Q$ 的直线，找到与椭圆曲线的交点。
  2. 该直线与椭圆曲线的第三个交点 $R’$。
  3. 将 $R’$ 关于 $x$ 轴对称得到点 $R$ 即为 $P + Q$ 的结果。

此外，推广一下能得到当$P=Q$时，两点的连线即为切线。以及$-P=(P_x,-P_y)$

那么根据加法运算的定义，可以推导出加法的计算方法

$$
K = \frac{y_P-y_Q}{x_P-x_Q}
$$

$$
R = P + Q = (K^2 – x_P – x_Q, – y_P + K(x_P – x_R))
$$

当$P=Q$时

$$
K = \frac{3x_P^2 + a}{2y_P}
$$

有了加法，就能很简单的推出乘法的计算了。但如果普通的不断加法计算乘法的话，时间复杂度是 $O(n)$ 的。于是可以利用二进制来实现快速乘法，这样时间复杂度就能降到 $O(\log n)$

例如，计算 $(101001)_2\cdot P$ 的时候可以计算出 $2^5\cdot P$，$2^3\cdot P$和$2^0\cdot P$ 然后相加就是要计算的乘法结果。

相似的，和一般意义上的群有生成元和群阶一样，对于这个椭圆曲线有限群，一样存在生成元，也称为基点，记作 $G$。也存在群阶，记作 $n$。

Montgomery 曲线

Montgomery 曲线通常是一个在平面上由关于 $x$ 和 $y$ 的方程定义的曲线，形式通常为

$$ By^2 = x^3 + Ax^2 + x $$

对于该曲线的加法运算有

$$ \alpha = \frac{(y_Q-y_P)}{x_Q-x_P} $$$$ R = P + Q = (B\alpha^2-A-x_P-x_Q,\alpha(x_P-x_R)-y_P) $$

同时，Montgomery 曲线也可以转化为 Weierstrass 曲线。对于

$$ By^2 = x^3 + Ax^2 + x \mapsto y^2 = x^3 + ax + b $$$$ (x,y) \mapsto \left(\frac{1}{B}x+\frac{A}{3B},\frac{1}{B}y\right) $$

于是有

$$ a=\frac{3-A^2}{3B^2},b=\frac{2A^3-9A}{27B^3} $$

椭圆曲线加密

明白椭圆曲线的一些基本概念之后，就可以开始探究 ECC 的原理了

  1. 首先选定一个椭圆曲线 $E$ 和一个基点 $G$，假设这个椭圆曲线的群阶为 $n$。
  2. 选择一个私钥 $d$，计算出公钥 $P = dG$。
  3. 公开曲线 $E$、$G$、$p$，以及公钥 $P$
  4. 加密：选取一个随机数 $k$，计算出 $Q = kG$ 和 $C = M + kP$，得到加密结果$(Q,C)$。
  5. 解密：接收方使用私钥 $a$ 计算 $M = C – dQ$，得到明文 $M$。

ECC 的安全性基于椭圆曲线离散对数问题（ECDLP），即给定 $P$ 和 $Q$，计算出 $d$ 使得 $Q = dP$ 是一个困难的问题。

但是还是不乏有一些对于较小数情况下的 ECDLP 算法，下文讲讲解常见的三种 DLP 算法。

常用算法

ps.下述的算法在不同领域有很多不同的变体但核心思想是一致的

  1. 大整数的分解
  2. 离散对数的求解
  3. 椭圆曲线上的离散对数求解

BSGS

1.离散对数

对于这样的一个式子$g^x=h\ mod\ m$对于一般暴力算法的复杂度是$O(\varphi(m))$，对于较大m会计算困难。于是有BSGS算法将复杂度减小到$O(\sqrt{m})$。个人认为其算法思想和MITM攻击类似。

主要操作如下，先将等式变化

$$g^{A\left \lceil \sqrt{m}\right \rceil-B}=h\ mod\ m$$

$$g^{A\left \lceil \sqrt{m}\right \rceil}=hg^B\ mod\ m$$

对等式右边遍历$B(B<\sqrt{m})$并打表，然后遍历等式左侧的A遍历并且找到相同的值，返回解$A\left \lceil \sqrt{m}\right \rceil-B$

def bsgs(g,h,p):
    tmp = ceil(sqrt(p))
    bs = {}
    for B in range(tmp):
        bs[h*pow(g,B,p)%p] = B
    tmp1 = pow(g,tmp,p)
    for A in range(tmp):
        if pow(tmp1,A,p) in bs:
            return A*tmp - bs[pow(g,tmp*A,p)]

修改了一下如果x的大小是已知的可以添加参数x最大值pi来减小复杂度

def bsgs(g,h,p,pi=None):
    if pi is None:
        pi = p
    tmp = ceil(sqrt(pi))
    bs = {}
    for B in range(tmp):
        bs[h*pow(g,B,p)%p] = B
    tmp1 = pow(g,tmp,p)
    for A in range(tmp):
        if pow(tmp1,A,p) in bs:
            return A*tmp - bs[pow(g,tmp*A,p)]

2.椭圆曲线

对于$Q=xP$，相似的可以得到

$$P=(a\left \lceil \sqrt{m}\right \rceil+b)G$$

$$P-bG=a\left \lceil \sqrt{m}\right \rceil G$$

同理

def bsgs(G,P,p,pi=None):
    if pi == None:
        pi = p
    tmp = ceil(sqrt(pi))
    bs = {}
    for b in range(tmp):
        bs[P-b*G] = b
    tmp1 = G*tmp
    for a in range(tmp):
        if tmp1*a in bs:
            return a*tmp+bs[tmp1*a]

Pollard rho

这个算法其实有点运用了🐒算法即随机游走

1.大整数分解

🐒算法体现在构造了一个环上的伪随机生成函数例如$f(x)=x^2+c\ mod\ n$，将这个函数用作递推数列产生不断的随机数。由于是在有限域上所以必定最终随机数会进入循环。易得当$x\equiv y$时，$f(x)\equiv f(y)$。

可以使用 Floted 算法判环。在一个ρ形图中，可以使用两个指针x、y，每次让x前进一步，y 前进两步，如果x和y重合了，就说明有环。同时可以对x，y计算gcd判断来猜测是否存在因数

def pollard_rho(n):
    c = random.randint(1, n-1)
    f = lambda x: (x*x + c) % n

    x, y, d = 0, 0, 1
    while d == 1 or d == n:
        x = f(x)
        y = f(f(y))
        if x == y:
            return pollard_rho(n)
        d = GCD(abs(x - y), n)
    return d

拓展一下有这样的分解因数算法

def factor(n):
    factors = []
    while n != 1:
        p = pollard_rho(n)
        times = 0
        while n % p == 0:
            n //= p
            times += 1
        factors.append((p,times))
    return factors

2.离散对数

对于$g^x\equiv h \mod p$，类似的使用相似的思想，先令$x\equiv g^ah^b\mod n$，我们会试图构造一个关于$x$生成函数，同时使用分区映射（为了快速游走，且满足良好的随机性），将整个群$G$分成数量大致相同的三部分$S$，最终得到这样的生成函数

$$ f(x)=f(\varphi(a,b))=\left\{\begin{matrix} \varphi(2a,2b) & x\in S_1 \\ \varphi(a+1,b) & x\in S_2 \\ \varphi(a,b+1) & x\in S_3 \\ \end{matrix}\right. $$

然后同样的使用 Floted 算法判环，寻找到$\varphi(a_1,b_1)=\varphi(a_2,b_2)$，基于对$x$的构造，可以推导出

$$ \begin{matrix} & \varphi(a_1,b_1) & \equiv & \varphi(a_2,b_2) & \mod p \\ \Rightarrow & g^{a_1}h^{b_1} & \equiv & g^{a_2}h^{b_2} & \mod p \\ \Rightarrow & g^{a_1-a_2} & \equiv & g^{x(b_2-b_1)} & \mod p \\ \Rightarrow & x & \equiv & \frac{a_1-a_2}{b_2-b_1} & \mod ord(g) \end{matrix} $$

下面是示范用的代码实现，不保证一定有解。

def pollard_rho(g, h, p, o=None):
    if o is None:
        o = p - 1
    f = lambda x, a, b: (x**2%p,2*a,2*b) if x%3 == 0 else ((x*g%p,a+1,b) if x%3 == 1 else (x*h%p,a,b+1))
    phi = lambda a,b: pow(g, a, p) * pow(h, b, p) % p
    a1,b1 = random.randint(0, o),random.randint(0, o)
    x1 = phi(a1,b1)
    x2,a2,b2 = f(x1,a1,b1)
    while x1 != x2:
        x1,a1,b1 = f(x1,a1,b1)
        x2,a2,b2 = f(*f(x2,a2,b2))

    gcd = lambda a,b: gcd(b,a%b) if b else a
    tmp = gcd(o, abs(b2-b1))
    if (a1-a2) % tmp != 0:
        return pollard_rho(g, h, p, o)
    res = ((a1-a2)//tmp)*pow((b2-b1)//tmp,-1,o//tmp) % (o//tmp)
    return res

⚠ 该代码在指定底数的阶的时候一定有解，但是当阶未知的时候，会使用群阶作为元素的阶，此时可能出现无解，所以使用随机初始状态来尝试多个不同的环，来保证能输出解。此外阶未知时，输出的解只能保证$res\equiv x \mod ord(g)$

3.椭圆曲线

同样的使用类似的思想，对于$P=x\cdot G$，先令$X=a\cdot G+b\cdot P$，然后类似的构造相同的函数$f(x)$

$$ f(X)=f(\varphi(a,b))=\left\{\begin{matrix} \varphi(2a,2b) & x\in S_1 \\ \varphi(a+1,b) & x\in S_2 \\ \varphi(a,b+1) & x\in S_3 \\ \end{matrix}\right. $$

并且使用 Floted 算法判环，寻找到$X_1=X_2$，基于对$X$的构造，可以推导出

$$ \begin{matrix} & \varphi(a_1,b_1) & \equiv & \varphi(a_2,b_2) & \mod p \\ \Rightarrow & {a_1}\cdot G+{b_1}\cdot P & \equiv & {a_2}\cdot G+{b_2}\cdot P & \mod p \\ \Rightarrow & (a_1-a_2)\cdot G & \equiv & (b_2-b_1)x\cdot G & \mod p \\ \Rightarrow & x & \equiv & \frac{a_1-a_2}{b_2-b_1} & \mod ord(G) \end{matrix} $$

下面是示范用的代码实现

def pollard_rho(E, G, P, o=None):
    if o == None:
        o = E.order()
    f = lambda X, a, b: (2*X, 2*a, 2*b) if int(X[0])%3 == 0 else ((X+G, a+1, b) if int(X[0])%3 == 1 else (X+P, a, b+1))
    phi = lambda a,b: a*G + b*P
    a1,b1 = random.randint(0, o), random.randint(0, o)
    X1 = phi(a1, b1)
    X2,a2,b2 = f(X1, a1, b1)
    while X1 != X2:
        X1,a1,b1 = f(X1, a1, b1)
        X2,a2,b2 = f(*f(X2, a2, b2))
    
    R.<x> = PolynomialRing(Zmod(o))
    f = (b2-b1)*x - (a1-a2)
    res = f.roots(multiplicities=False)
    if len(res) > 1e6:  # 限制增根数量
        return pollard_rho(E, G, P, o)
    for i in res:
        if i*G == P:
            return i
    else:
        return pollard_rho(E, G, P, o)

这里把反求x的过程使用了Sage的求根运算，因为我们只能保证x是该多项式的一个根，而不是唯一的根，同时防止大素数p导致增根数量过多，这里限制为1e6。

Pohlig-Hellman

1.离散对数

条件：$p$为质数，且$\varphi(p)$是光滑数

对于$a^x=b\ mod\ p$，确定原根g，可以转化为$g^{ux}=g^v\ mod\ p$

也就是$x=v\cdot u^{-1}\ mod\ p-1$，因此只需要计算出u，v即可解的x

下面推导如何计算$g^u=a\ mod\ p$中的u

对于$p-1$可以分解因数得到$p-1=p_1^{q_1}p_2^{q_2}\cdots p_n^{q_n}$

可以构造$u$使得满足$u=c_0p_1^0+c_1p_1^1+c_2p_1^2+\cdots+c_{q_1-1}p_1^{q_1-1}\ mod\ p_1^{q_1}$

于是就有

$$ \left\{\begin{matrix} u=c_0+c_1p_1+c_2p_1^2+&\cdots&+c_{q_1-1}p_1^{q_1-1}\ mod\ p_1^{q_1}\\ u=c_0’+c_1’p_2+c_2’p_2^2+&\cdots&+c_{q_2-1}’p_2^{q_2-1}\ mod\ p_2^{q_2}\\ &\cdots&\\ u=c_0^{”}+c_1^{”}p_3+c_2^{”}p_3^2+&\cdots&+c_{q_3-1}^{”}p_3^{q_3-1}\ mod\ p_3^{q_3}\\ \end{matrix}\right. $$

求解每个同余方程的c再用crt合并即可得到

下面解c

构造此式子$(g^u)^{\frac{p-1}{p_1^r}}=a^{\frac{p-1}{p_1^r}}\ mod\ p$

于是令$r=1$时有$g^{c_0\frac{p-1}{p_1}}=a^{\frac{p-1}{p_1}}\ mod\ p$

此时只需要爆破即可解出$c_0$，且p是光滑数，显然爆破是可行的

接着调整$r=2$，同理爆破就可以得到$c_1$

所有c解出来之后用crt合并即可得到u

然后回代上式，得到x

from Crypto.Util.number import *
from sage.all import *

def Pohlig_Hellman(a, b, p):
    g = int(GF(p).primitive_element())
    factors = list(factor(p-1))
    mods = [a**b for a,b in factors]
    def cal(a):
        residues = []
        for i in range(len(factors)):
            tmp = 0
            tmp1 = pow(g,(p-1)//factors[i][0],p)
            cs = []
            for r in range(1,factors[i][1]+1):
                tmp2 = pow(g,tmp,p)
                tmp3 = pow(a,(p-1)//factors[i][0]**r,p)
                for c in range(factors[i][0]):
                    if tmp2*pow(tmp1,c,p) == tmp3:
                        cs.append(c)
                        tmp += c*(p-1)//factors[i][0]
                        tmp //= factors[i][0]
                        break
            residues.append(sum(c*factors[i][0]**k for k,c in enumerate(cs))%mods[i])
        u = crt(residues,mods)

        return u
    
    u = cal(a)
    v = cal(b)

    if GCD(u,p-1) == 1:
        return v*pow(u,-1,p-1)
    else:
        tmp = 1
        while True:
            gcd = GCD(u,p-1)
            if gcd == 1:
                break
            tmp *= gcd
            u //= gcd
        return ZZ(v*pow(u,-1,p-1))//tmp

if __name__ == '__main__':
    p = 7863166752583943287208453249445887802885958578827520225154826621191353388988908983484279021978114049838254701703424499688950361788140197906625796305008451719
    a = getRandomNBitInteger(256)
    x = getRandomNBitInteger(256)
    b = pow(a,x,p)

    print(x) 
    print(Pohlig_Hellman(a, b, p))

ps.在暴破c的时候还有一说可以用BSGS来优化算法，如下

# Sample
# BSGS & Pohlig_Hellman for DLP

from Crypto.Util.number import *
from sage.all import *

def bsgs(g,h,p,pi):
    if pi == None:
        pi = p
    tmp = ceil(sqrt(pi))
    bs = {}
    for B in range(tmp):
        bs[h*pow(g,B,p)%p] = B
    tmp1 = pow(g,tmp,p)
    for A in range(tmp):
        if pow(tmp1,A,p) in bs:
            return A*tmp - bs[pow(g,tmp*A,p)]

def Pohlig_Hellman(a, b, p):
    g = int(GF(p).primitive_element())
    factors = list(factor(p-1))
    mods = [a**b for a,b in factors]

    def cal(a):
        residues = []
        for i in range(len(factors)):
            tmp = 0
            tmp1 = pow(g,(p-1)//factors[i][0],p)
            cs = []
            for r in range(1,factors[i][1]+1):
                tmp2 = pow(a,(p-1)//factors[i][0]**r,p)*pow(g,-tmp,p)
                c = bsgs(tmp1,tmp2,p,factors[i][0])
                cs.append(c)
                tmp += c*(p-1)//factors[i][0]
                tmp //= factors[i][0]
            residues.append(sum(c*factors[i][0]**k for k,c in enumerate(cs))%mods[i])
        u = crt(residues,mods)

        return u
    
    u = cal(a)
    v = cal(b)

    if GCD(u,p-1) == 1:
        return v*pow(u,-1,p-1)
    else:
        tmp = 1
        while True:
            gcd = GCD(u,p-1)
            if gcd == 1:
                break
            tmp *= gcd
            u //= gcd
        return ZZ(v*pow(u,-1,p-1))//tmp

if __name__ == '__main__':
    p = 7863166752583943287208453249445887802885958578827520225154826621191353388988908983484279021978114049838254701703424499688950361788140197906625796305008451719
    a = getRandomNBitInteger(256)
    x = getRandomNBitInteger(512)
    b = pow(a,x,p)

    print(x) 
    print(Pohlig_Hellman(a, b, p))

2.椭圆曲线

大致思想和DLP相同

对于椭圆曲线上$P=kG$求解$k$时

先确定G基点的阶n，即nG=0，然后同样的对进行因式分解，得到$n=p_1^{q_1}p_2^{q_2}\cdots p_n^{q_n}$

相似的构造如下的同余方程组

$$ \left\{\begin{matrix} k=c_0+c_1p_1+c_2p_1^2+&\cdots&+c_{q_1-1}p_1^{q_1-1}\ mod\ p_1^{q_1}\\ k=c_0’+c_1’p_2+c_2’p_2^2+&\cdots&+c_{q_2-1}’p_2^{q_2-1}\ mod\ p_2^{q_2}\\ &\cdots&\\ k=c_0^{”}+c_1^{”}p_3+c_2^{”}p_3^2+&\cdots&+c_{q_3-1}^{”}p_3^{q_3-1}\ mod\ p_3^{q_3}\\ \end{matrix}\right. $$

同理，构造此式子$\frac{n}{p_1^r}P=\frac{n}{p_1^r}nG\ mod\ p$

当$r=1$时有$\frac{n}{p_1}P=c_0\frac{n}{p_1}G$

爆破即可解出c然后依次遍历r

crt合并恢复k

# Sample
# BSGS & Pohlig_Hellman for ECDLP

from Crypto.Util.number import *

def bsgs(G,P,p):
    tmp = ceil(sqrt(p))
    bs = {}
    for b in range(tmp):
        bs[P-b*G] = b
    tmp1 = G*tmp
    for a in range(tmp):
        if tmp1*a in bs:
            return a*tmp+bs[tmp1*a]

def Pohlig_Hellman(G,P):
    n = G.order()
    factors = list(factor(n))
    mods = []
    residues = []
    for i in range(len(factors)):
        if factors[i][0] > 10**9:
            break
        tmp = 0
        tmp1 = G*(n//factors[i][0])
        cs = []
        for r in range(1,factors[i][1]+1):
            tmp2 = P*(n//factors[i][0]**r)-G*tmp
            c = bsgs(tmp1,tmp2,factors[i][0])
            cs.append(c)
            tmp += c*n//factors[i][0]
            tmp //= factors[i][0]
        log = sum(c*factors[i][0]**k for k,c in enumerate(cs))%(factors[i][0]**factors[i][1])
        print(log)
        residues.append(log)
        mods.append(factors[i][0]**factors[i][1])
    k = crt(residues,mods)

    return k

感觉对于较大的数e7~e9计算有点慢，似乎是BSGS本身复杂度的问题，但我尝试用sage内置的对数运算却报错显示无解，真复杂，最后还是用自己的BSGS算了

Lazzaro大佬的板子，将BSGS的部分替换成sage内置的对数运算了

这个板子很快不知道为什么

E = EllipticCurve(GF(p), [a, b])
P = 
Q = 

n = E.order()

factors = list(factor(n))
m = 1
moduli = []
remainders = []

print(f"[+] Running Pohlig Hellman")
print(factors)

for i, j in factors:
    if i > 10**9:
        print(i)
        break
    mod = i**j
    g2 = P*(n//mod)
    q2 = Q*(n//mod)
    r = discrete_log(q2, g2, operation='+')
    remainders.append(r)
    moduli.append(mod)
    m *= mod

r = crt(remainders, moduli)
print(r)

这个也很慢

E = EllipticCurve(GF(p), [a, b])
P = 
Q = 

factors, exponents = zip(*factor(E.order()))
primes = [factors[i] ^ exponents[i] for i in range(len(factors))]
print(primes)
dlogs = []
for fac in primes:
	t = int(int(P.order()) // int(fac))
	dlog = discrete_log(t*Q,t*P,operation="+")
	dlogs += [dlog]
	print("factor: "+str(fac)+", Discrete Log: "+str(dlog)) #calculates discrete logarithm for each prime order

l = crt(dlogs,primes)
print(l)

Shor 量子算法

咕咕ing

ECDH

ECDH 是 Diffie-Hellman 密钥交换算法在椭圆曲线上的实现。其原理与 DH 密钥交换算法类似。

  1. Alice 和 Bob 选择一个椭圆曲线 $E$ 和一个基点 $G$。
  2. Alice 选择一个私钥 $a$，计算出公钥 $A = aG$，并将 $A$ 发送给 Bob。
  3. Bob 选择一个私钥 $b$，计算出公钥 $B = bG$，并将 $B$ 发送给 Alice。
  4. Alice 接收到 Bob 的公钥后，计算出共享密钥 $K_A = bA$。
  5. Bob 接收到 Alice 的公钥后，计算出共享密钥 $K_B = aB$。
  6. 最终，Alice 和 Bob 都得到了相同的共享密钥 $K = abG$。

常见攻击

Smart’s attack

条件：$E.order()=p$

def SmartAttack(P,Q,p):
    E = P.curve()
    Eqp = EllipticCurve(Qp(p, 2), [ ZZ(t) + randint(0,p)*p for t in E.a_invariants() ])

    P_Qps = Eqp.lift_x(ZZ(P.xy()[0]), all=True)
    for P_Qp in P_Qps:
        if GF(p)(P_Qp.xy()[1]) == P.xy()[1]:
            break

    Q_Qps = Eqp.lift_x(ZZ(Q.xy()[0]), all=True)
    for Q_Qp in Q_Qps:
        if GF(p)(Q_Qp.xy()[1]) == Q.xy()[1]:
            break

    p_times_P = p*P_Qp
    p_times_Q = p*Q_Qp

    x_P,y_P = p_times_P.xy()
    x_Q,y_Q = p_times_Q.xy()

    phi_P = -(x_P/y_P)
    phi_Q = -(x_Q/y_Q)
    k = phi_Q/phi_P
    return ZZ(k)
[1] Smart N P. The discrete logarithm problem on elliptic curves of trace one[J]. Journal of cryptology, 1999, 12: 193-196.

MOV attack

条件：$E.order()=p+1$

使用双线性配对，使得原 ECDLP 问题变为了 DLP 问题，最重要的意义在于实质证明了 ECDLP 问题与 DLP 问题是等价的。

a =
b =
p =
Fp = GF(p)
E = EllipticCurve(Fp, [a, b])
G = E(, )
P = E(, )

order = E.order()
k = 1
while (p**k - 1) % order:
    k += 1

K.<a> = Fp.extension(k)
EK = E.base_extend(K)
PK = EK(P)
GK = EK(G)
QK = EK.lift_x(a + 3)  # Independent from PK
AA = PK.tate_pairing(QK, E.order(), k)
GG = GK.tate_pairing(QK, E.order(), k)
r = AA.log(GG)
print(r)
[2] Menezes A, Vanstone S, Okamoto T. Reducing elliptic curve logarithms to logarithms in a finite field[C]//Proceedings of the twenty-third annual ACM symposium on Theory of computing. 1991: 80-89.

Invalid Curve Attack

无效曲线攻击（Invalid Curve Attack）是一种针对椭圆曲线密码学（ECC）的攻击方法，主要利用了靶机在对于传入的点没有验证其正确性，造成的安全性漏洞。

这个攻击通常发生在 ECDH 密钥交换过程中，攻击者可以通过发送一个无效的椭圆曲线点来破坏密钥交换的安全性。

基于 ECDH，我们可以知道，当我们向靶机发送一个点的时候，靶机会计算这个点和私钥的乘积并返回计算结果。

假如当我们选取了一个无效的点 $P$，并且根据椭圆曲线上的加法定义可以显然得到在计算乘法的时候完全和 $b$ 的取值无关，因此返回的点一定是在该无效曲线上的

于是可以尝试构造出一个带有小阶的无效点 $P$，然后通过计算 $kP$ 的方式来得到点 $Q$，那么就能很容易得到 $k’ = k \mod P.order()$

当有足够数量的同余式后，用 CRT 合并即可得到靶机的私钥

CryptoECC

评论

  1. ink
    6 天前
    2025-9-09 23:07:50

    Sean神！！

  4. Marinaco
    6 月前
    2025-3-24 22:20:16

    sean神(๑•̀ㅁ•́ฅ)

  7. 茗辰原
    6 月前
    2025-3-22 19:54:11

    我来喽!

发送评论 编辑评论

























|´・ω・)ノ
ヾ(≧∇≦*)ゝ
(☆ω☆)
（╯‵□′）╯︵┴─┴
￣﹃￣
(/ω＼)
∠( ᐛ 」∠)＿
(๑•̀ㅁ•́ฅ)
→_→
୧(๑•̀⌄•́๑)૭
٩(ˊᗜˋ*)و
(ノ°ο°)ノ
(´இ皿இ｀)
⌇●﹏●⌇
(ฅ´ω`ฅ)
(╯°A°)╯︵○○○
φ(￣∇￣o)
ヾ(´･ ･｀｡)ノ"
( ง ᵒ̌皿ᵒ̌)ง⁼³₌₃
(ó﹏ò｡)
Σ(っ °Д °;)っ
( ,,´･ω･)ﾉ"(´っω･｀｡)
╮(╯▽╰)╭
o(*////▽////*)q
＞﹏＜
( ๑´•ω•) "(ㆆᴗㆆ)
😂
😀
😅
😊
🙂
🙃
😌
😍
😘
😜
😝
😏
😒
🙄
😳
😡
😔
😫
😱
😭
💩
👻
🙌
🖕
👍
👫
👬
👭
🌚
🌝
🙈
💊
😶
🙏
🍦
🍉
😣
Source: github.com/k4yt3x/flowerhd
颜文字
Emoji
小恐龙
花!



上一篇
下一篇